Exercícios Resolvidos de Capacitância Equivalente

Exercício 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

Enunciado

Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 25 – seção 4 - Problema 15.

(Cap 25 Ex- 15) Na Fig. 25-31 , uma bateria de 20,0 V é ligada a um circuito constituído por capacitores de capacitâncias e . Determine (a) a capacitância equivalente do circuito; (b) a carga armazenada por ; (c) e (d) do capacitor 1; (e) e (f) do capacitor 2; (g) e (h) do capacitor 3.

Passo 1

Falaaii meus amores, tudo certinho?

Bora resolver comigo mais uma??

Para resolver esse circuito, podemos ir reduzindo ele aos poucos. De cara, temos que os capacitores e estão em série, assim:

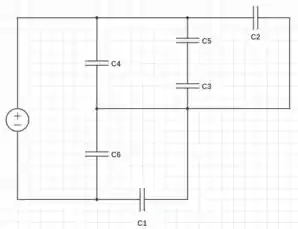Figura SEQ Figura \* ARABIC1

Se torna:

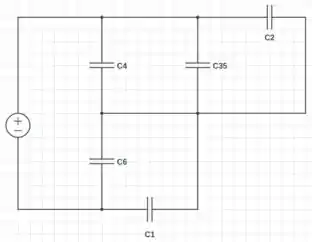Figura SEQ Figura \* ARABIC2

Podemos utilizar a formula para descobrir a capacitância de capacitores em série:

Agora, temos que e estão em paralelo, portanto:

Como eles estão em paralelo, basta somar suas capacitância:

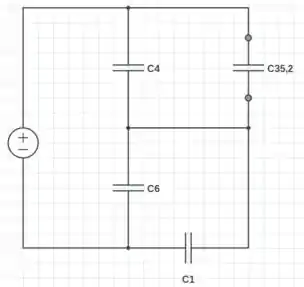Figura SEQ Figura \* ARABIC3

Agora, podemos ver que esta em paralelo com e esta em paralelo com , assim podemos reescrever o circuito:

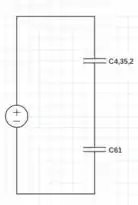Figura SEQ Figura \* ARABIC4

Esses capacitores tem capacitância de:

Agora, responde o item (a), basta calcular essa ultima capacitância. Como as capacitâncias e são iguais, o resultado de colocar elas em série é:

Passo 2

No item (b), a DDP que em cima da é 20,0 V, portanto para calcular a carga armazenada basta utilizar a formula:

Passo 3

Para responder ao item (c), vamos olhar para a figura 4, como os dois capacitores equivalentes tem a mesma capacitância a DDP da bateria é dividida igualmente entre eles, portanto há 10 V em cima de cada um. Como o capacitor é formado pelos capacitores e postos em paralelo a DDP em cima deles também é 10 V.

Passo 4

A carga em cima de do capacitor 1, item (d) é:

Passo 5

Olhando para a figura 2, vemos que os capacitores , e estão em paralelo. Portanto, a voltagem em cima deles é 10 V, que é a resposta do item (e).

Passo 6

Agora, para achar a carga em cima do capacitor 2, item (f):

Passo 7

Temos que a DDP em cima do capacitor é 10 V e os capacitores e tem a mesma capacitância, portanto, os 10 V são dividido igualmente nos dois. Assim, a resposta do item (g) é que a DDP em cima do capacitor é 5V.

Passo 8

Por ultimo, para calcular o item (h):

Resposta

(a)

(b)

(c)

(d)(e)

(f)

(g)

(h)

Exercícios de Livros Relacionados

Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota

Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica

Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e

Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.

Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .