Um capacitor de placas planas e paralelas, de área , a distância , é “recheado” por uma chapa condutora, também de área , e espessura .

A capacitância de tal capacitor é:
Passo 1
As fórmulas que precisamos para resolver o problema são:
- Capacitância de um capacitor de placas planas paralelas de área e distância entre as placas;
- Capacitância de associação em série de dois capacitores;
- Capacitância de associação em paralelo de dois capacitores;
Passo 2
Agora, para entender o que acontece com a capacitância precisamos entender que tipo de capacitor novo nós temos. A ideia de capacitor é você conseguir separar cargas opostas por um certo espaço. Como antes nós tínhamos a seguinte configuração:
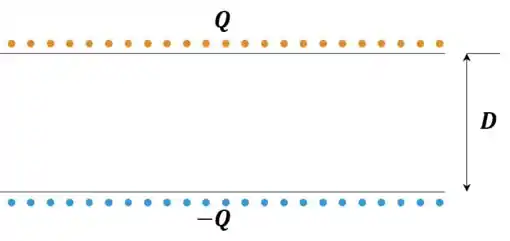
Quando inserimos uma placa condutora nesse meio, as cargas que já haviam lá (i.e. e ) vão induzir cargas na placa: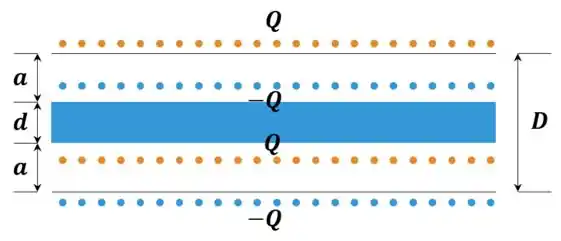
Passo 3
Portanto podemos perceber que temos dois capacitores. Agora, em série ou paralelo? Para algumas pessoas isso não é óbvio então vamos de volta ao nosso macete:
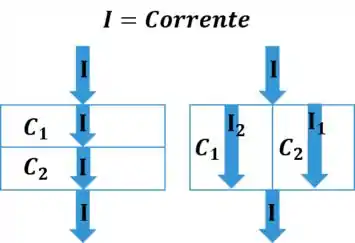
Ou seja, se a corrente “se dividir” em dois caminhos nós temos um caso de capacitores em paralelo. Se ela segue um caminho só temos série. No nosso caso temos então uma associação em série de capacitores.
Passo 4
Além disso os dois tem a mesma distância entre as placas e a mesma área, portanto:
Substituindo a fórmula de capacitores de placas planas paralelas:
Resposta
Letra c