Para o sistema de capacitores mostrado na figura abaixo, encontre a capacitância equivalente
(a) entre e ; e
(b) entre e .
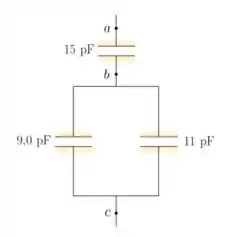
Passo 1
(a) Encontre a capacitância equivalente entre e .
Entre os terminais e , temos dois capacitores em paralelo, certo? Nesse caso, então, a capacitância equivalente é dada por:
Passo 2
(b) Encontre a capacitância equivalente entre e .
Aqui podemos pensar que temos dois capacitores em série: o capacitor de entre os terminais e e um capacitor entre os terminais e , com capacitância calculada no item (a).
Se estão em série, a capacitância equivalente será dada por:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e
Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .