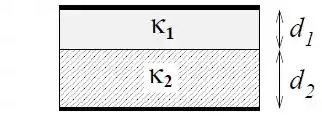
Um capacitor de placas paralelas e área , possui o espaço entre as placas preenchido por materiais dielétricos de diferentes constantes dielétricas ( e ), arranjados em diferentes espessuras ( e , respectivamente), como mostra a figura.
Calcule a capacitância de um capacitor de placas paralelas de área e distância entre placas, onde há vácuo, igual a . Dado: o campo elétrico entre as placas do capacitor é .
Calcule a capacitância do capacitor da figura.
A placa superior do capacitor está a um potencial 0 em relação à placa inferior. Determine a densidade de cargas livres na placa superior deste capacitor, e a densidade de cargas ligadas (ou induzidas) na face do dielétrico em contato com esta placa.
Passo 1
Calcule a capacitância de um capacitor de placas paralelas de área e distância entre placas, onde há vácuo, igual a . Dado: o campo elétrico entre as placas do capacitor é .
A relação entre a capacitância e o potencial é dada por:
O potencial entre as placas do capacitor é dado por:
Substituindo na expressão da capacitância:
O próprio problema já nos disse para considerar , em que é a densidade superficial de carga, dada por , onde é a área da placa do capacitor.
Voltando ao problema:
Finalmente:
Essa é uma fórmula que é importante você já ter na cabeça, mas é muito importante também você lembrar como se chega nela.
Passo 2
Calcule a capacitância do capacitor da figura.
Eu sei que a figura pode parecer meio bizarra, mas vamos tentar imaginar o seguinte: imagina que vem uma corrente de cima para baixo... teoricamente, ela passaria primeiro pelo dielétrico e, posteriormente, pelo dielétrico . Assim, podemos imaginar então que esses dois dielétricos estão, na verdade, em série.
E a capacitância do capacitor será a capacitância equivalente para esses dois capacitores em série. Quando os capacitores estão em série, a capacitância equivalente é dada por:
A capacitância de um capacitor com o dielétrico é dado por:
Logo:
Agora é só arrumar esse cara:
Passo 3
A placa superior do capacitor está a um potencial 0 em relação à placa inferior. Determine a densidade de cargas livres na placa superior deste capacitor, e a densidade de cargas ligadas (ou induzidas) na face do dielétrico em contato com esta placa.
Para a densidade de cargas livres, podemos simplesmente usar a relação .
Passo 4
Ok, agora precisamos calcular a densidade de cargas induzidas na placa superior, que está em contato com o dielétrico .
Definindo que para cima será positivo, o campo elétrico no dielétrico é dado por:
Essa variação do campo elétrico acontece porque, com o dielétrico temos dois campo existentes na região... o campo original e o campo induzido , que está na direção oposta, logo:
Agora é só isolar .
Resposta