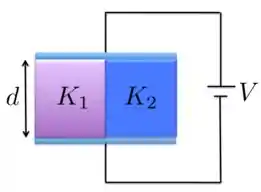
Um capacitor com placas paralelas possui o espaço entre as placas preenchido com duas camadas de dielétricos, uma com constante dielétrica e a outra com a constante dielétrica , como mostra a Figura abaixo. Cada camada possui espessura igual à distância entre as placas e cada camada preenche o espaço entre as placas. Se as placas são mantidas à uma diferença de potencial fixa , então mostre que capacitância é dada por
Passo 1
Neste caso, como as placas do capacitor são mantidas a uma diferença de potencial fixa , isso significa que podemos tratar o capacitor como se fosse uma associação em paralelo de dois capacitores, um com capacitância e dielétrico e outro com dielétrico , ambos com área de superfície das placas igual a e separadas por .
Por isso, temos o seguinte:
Agora, como a capacitância aumenta de um fator constante quando o capacitor é preenchido com um dielétrico e a área de cada um desses “capacitores” é , teremos