Um capacitor é formado por duas placas condutoras planas e paralelas de área cada uma, separadas por uma distância muito menor que as suas dimensões. Um material isolante de constante dielétrica é inserido no capacitor de forma a ocupar metade do volume entre as placas, como mostrado na figura abaixo, ficando completamente em contato com uma delas, enquanto a outra metade permanece no vácuo. A seguir, uma diferença de potencial é aplicada entre as placas. Em termos de e , determine para esse sistema:
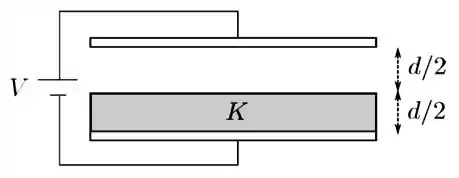
- A capacitância do sistema.
- Os módulos do campo elétrico na metade vazia () e na metade com dielétrico ().
Passo 1
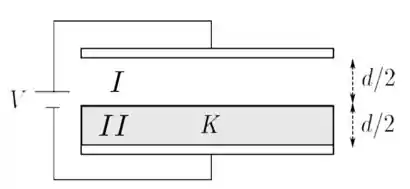
- No caso particular desta questão, podemos analisar sua capacitância como se fosse resultado de uma associação em série de dois capacitores, um com capacitância , com vácuo entre suas placas, e outro com capacitância , no qual há um dielétrico com constante dielétrica , como indicado na figura abaixo.
- Para calcularmos como é o campo em cada região, precisamos da carga total armazenada no capacitor . Neste caso, a carga total é
Portanto, essa capacitância resultante neste caso é
Como o capacitor está no vácuo (espaço vazio entre suas placas), sua capacitância é dada por
O capacitor , por sua vez, possui um dielétrico com constante dielétrica e tem capacitância dada por
Substituindo essas expressões em , temos
Passo 2
Na região do capacitor, “que tem o vácuo” (região vazia entre as placas), o campo elétrico , após substituir a densidade de carga acima, é
Na região do capacitor, o campo elétrico é menor que por um fator , isto é,
o que resulta em
Resposta
a)
b) ;