Exercícios Resolvidos de Capacitância Equivalente

Exercício 9 1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

Enunciado

UFRJ- Física 3 – P1 2018.1 - DIURNO - 5

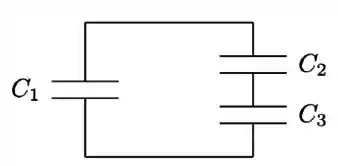
Um capacitor de capacitância é conectado inicialmente a uma bateria e carregado até armazenar uma carga . A seguir, o capacitor é desconectado da bateria e conectado a dois outros capacitores, inicialmente descarregados, de capacitâncias e , como mostrado na figura abaixo. Nessa nova configuração, após restabelecido o equilíbrio eletrostático, o capacitor armazena uma carga . Nessa situação, as cargas armazenadas nos capacitores e valem, respectivamente:

e

e

e

e

e

e

Passo 1

Como descrito pelo enunciado, o capacitor tem uma carga após restabelecido o equilíbrio eletrostático.

A presença da carga positiva na placa superior de produz um campo elétrico que atrai as cargas negativas para a placa inferior deixando-a com carga negativa . Isso faz com que a placa inferior de fique carregada positivamente com e a superior com

Consequentemente, a placa inferior de tem carga e a superior . Por isso, cada capacitor terá uma carga de .

Essa é a explicação do porquê em uma associação em série de capacitores temos todos os capacitores com mesma carga.

Resposta

Letra a).

Exercícios de Livros Relacionados

Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota

Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica

Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e

Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.

Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .