No circuito da figura abaixo uma bateria fornece uma diferença de potencial e os capacitores todos possuem a mesma capacitância .
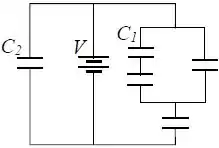
As cargas dos capacitores e são respectivamente:
; .
; .
; .
; .
; .
; .
Passo 1
O primeiro passo aqui é nomear os capacitores pra não nos enrolarmos com os cálculos:
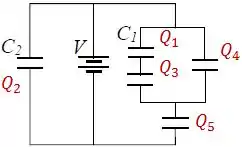
Em seguida, vamos analisar cada malha separadamente, lembrando que a diferença de potencial entre as placas de um capacitor é dada por:
Passo 2
Vamos olhar primeiro para , começando pela malha que contém a fonte e os capacitores de cargas , e .
Os capacitores em série possuem a mesma carga, logo:
Passo 3
Analisando a malha que contém somente os capacitores de cargas , e , teremos:
Como vimos no passo anterior, , logo:
Passo 4
A carga total para capacitores em paralelo é a soma das cargas, logo:
Como e estão em série:
Substituindo o que encontramos nos Passos 2 e 3, teremos:
Passo 5
Voltando na primeira equação do Passo 2, temos:
Substituindo o que encontramos nos passos anteriores, teremos:
Onde e . Logo:
Passo 6
Olhando para , temos que:
Substituindo os valores:
A resposta certa é a letra .
Resposta
; .