Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 25 – seção 4 - Problema 28.
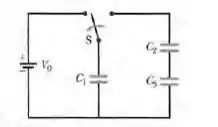
(Cap 25 Ex- 28) A Fig. abaixo mostra uma bateria de e três capacitares descarregados de capacitâncias , e . A chave é deslocada para a esquerda até que o capacitar 1 esteja totalmente carregado. Em seguida, a chave é deslocada para a direita. Determine a carga final (a) do capacitar 1; (b) do capacitar 2; (c) do capacitar 3.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Bem, os capacitores 2 e 3 estão em série e podem ser substituídos por um capacitor com capacitância igual a:
A carga do capacitor equivalente (chamaremos de é a mesma carga do capacitor 2 e 3, pois eles estão em série. Chamaremos as cargas do capacitor 2 e 3 de e . Então
.
A diferença de potencial entre os terminais do capacitor equivalente é
A diferença de potencial entre as placas do capacitor 1 é . Como a diferença de potencial entre as placas do capacitor equivalente é a mesma das placas do capacitor 1, pois eles estão em paralelo, então,
Passo 2
Quando a gente muda a chave para a direita, parte da energia do capacitor 1 vai para os capacitores 2 e 3. Vamos chamar de a carga inicial do capacitor 1, de acordo com a lei de conservação de energia, em que é a diferença de potencial original do capacitor 1.
Passo 3
Item (a)
Precisamos resolver o sistema de equações encontrados nos passos anteriores:
Substituindo pelos valores que temos no enunciado, obtemos
Passo 4
Item (b)
Como dito anteriormente,
Sabemos então que
Passo 5
Item (c)
Como a carga do capacitor 2 é igual a carga do capacitor 3, já que eles estão em série,