Dado o circuito abaixo:
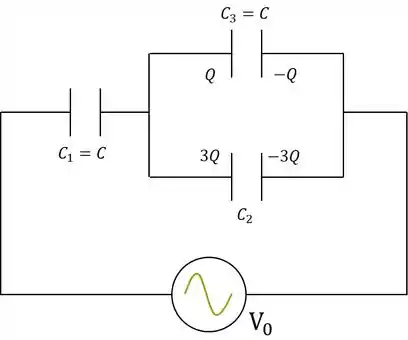
- Calcule a capacitância de em função da capacitância ;
- Calcule a capacitância equivalente do circuito todo em função da capacitância ;
Passo 1
Partiu então. Temos que na parte do circuito em que existem e paralelos, a carga em é três vezes maior que em :
Mas, ao mesmo tempo, eles estão em paralelo e portanto estão submetidos à mesma voltagem (não é a mesma que ). Dessa forma:
Dividindo ambas equações:
Substituindo o valor de :
Passo 2
Aplicando a fórmula de capacitores em paralelo:
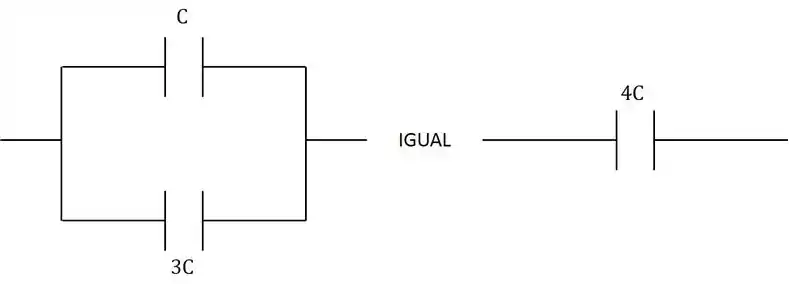
Ou seja, o circuito vira:
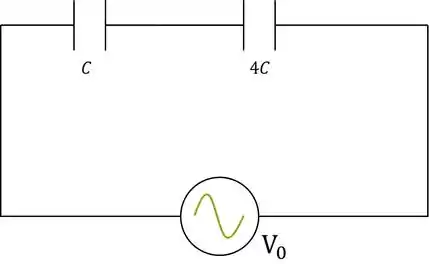
Aplicando agora a fórmula de capacitores em série:
Resposta
a)
b)
Exercícios de Livros Relacionados
Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e
Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .