UFRJ- Física 3 – P1 2018.2 - DIURNO - 7
Um capacitor de placas planas e paralelas de área , separadas por uma distância , possui uma capacitância quando há vácuo entre as placas. Por erro do fabricante, foi inserido no capacitor um material condutor, como mostrado na figura abaixo. Sabendo que a largura do material condutor vale e que os efeitos de borda podem ser desprezadas, a capacitância do sistema com o condutor dentro vale:
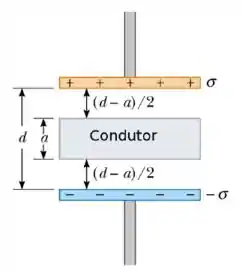
- 0
Passo 1
Como mostra a figura abaixo, a presença das cargas da placa superior do capacitor induzirá uma redistribuição de cargas negativas sobre a superfície superior do condutor. Por outro lado, as cargas do capacitor induzirão na superfície inferior do condutor cargas , de maneira que, no equilíbrio eletrostático, o campo elétrico dentro do condutor seja nula em todos os pontos do seu volume.
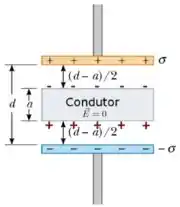
Olhando para essa figura, a gente vê tem dois capacitores em série, portanto com diferenças de potencial diferentes, e com mesmas cargas superficiais. Por isso, para encontrarmos qual seria a capacitância equivalente, temos que usar
Como esses dois capacitores têm a mesma capacitância, a expressão para fica ainda mais simples:
Mas,
Como o problema diz que , teremos, então, que
sendo que é a capacitância que o capacitor teria se não houvesse o condutor.
Resposta
Letra e.