Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Capacitância Equivalente

Ver Teoria
Exercício 33123456789101112131415161718192021222324252627282930313234

Enunciado

Origem da questão

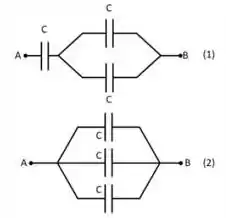
Considere os dois circuitos mostrados na figura abaixo. Todos os capacitores são idênticos e tem capacitâncias iguais a C . A diferença de potencial entre os terminais A e B também é a mesma. Sejam C 1 e C 2 as capacitâncias equivalentes dos circuitos 1 e 2 entre os terminais A e B respectivamente. Nessa situação, podemos afirmar que a razão C 1 / C 2 vale:

  1. 1
  2. 9 2
  3. 2 3
  4. 3 2
  5. 2 9

Passo 1

Falai gente, como vocês estão? Vamos lá? Como a questão quer saber a razão entre capacitâncias equivalentes, vamos calcular a de cada situação ok? Como capacitores só podem estar em série ou em paralelo, vamos usar essas duas equações:

1 C e q = ∑ 1 C                 E m   S é r i e C e q = ∑ C                 E m   P a r a l e l o

Partiu?

Passo 2

Pro caso 1 , temos:

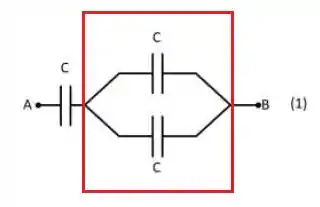
A gente pode primeiro fazer a capacitância equivalente da parte marcada, que está em paralelo em! Vamos obter então:

C * = C + C = 2 C

E ai o problema ganha uma nova cara:

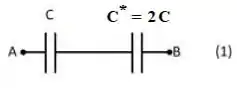
Com esses em série, podemos calcular a capacitância equivalente usando a fórmula em série:

1 C 1 = 1 C + 1 C * = 1 C + 1 2 C = 2 2 C + 1 2 C = 3 2 C

C 1 = 2 3 C

Passo 3

Agora pro caso 2 , se fizermos pros capacitores em paralelo marcados abaixo primeiro:

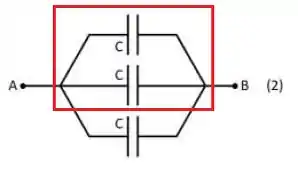
Achamos a seguinte capacitância equivalente:

C * = C + C = 2 C

Show galera, agora o problema ficou assim:

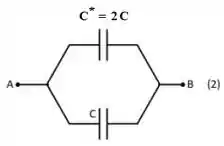
Então fechamos a capacitância equivalente do caso 2 ! Basta usar a fórmula pro caso em paralelo uma última vez:

C 2 = C + C * = C + 2 C = 3 C

Passo 4

Pra fechar, bora juntar os resultados! Temos:

C 1 = 2 3 C

C 2 = 3 C

Perfeito! A razão C 1 / C 2 vai valer então:

C 1 C 2 = 2 3 C 3 C = 2 9

A letra que corresponde a isso é a Letra E !

Resposta

L e t r a   E

Exercícios de Livros Relacionados

Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e
Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .