Unicamp, Física 3, 2019.2, P1, Questão 9.
Usa-se uma bateria para carregar uma combinação de dois capacitores indênticos ligados em paralelo. Se a diferença de potencial nos terminais da bateria é e uma carga total flui pela bateria durante o processo de carga, então a carga em cada capacitor e a diferença de potencial através de cada um são:
a) e , respectivamente
b) e , respectivamente
c) e , respectivamente
d) e , respectivamente
e) e , respectivamente
Passo 1
Vamos dar uma olhada em um circuito de dois capacitores em paralelo:
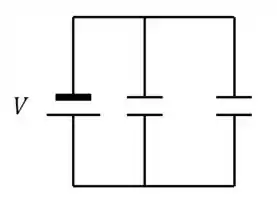
Duas coisas importantes que a gente precisa lembrar sobre capacitores em paralelo.
Primeiro, a diferença de potencial é a mesma entre as placas de todos os capacitores.
Segundo, a carga total armazenada nos capacitores é a soma das cargas em cada capacitor.
Passo 2
Então beleza, de cara já ficamos só com as alternativas (a) e (c), porque só elas dizem que o potencial em cada capacitor é .
E como os capacitores são idênticos, a carga vai se dividir igualmente entre eles. Ou seja:
Então a resposta correta é a letra (c). A carga se divide e o potencial é o mesmo.
Resposta
Letra (c).