Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Capacitância Equivalente

Ver Teoria
Exercício 17123456789101112131415161819202122232425262728293031323334

Enunciado

a) Determine a capacitância associada a um capacitor de placas paralelas, quadradas, de lado L , separadas por uma distância d (onde d < < L ) para o caso em que o espaço entre as placas está ocupado pelo vácuo.

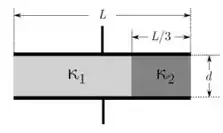
b) Suponha agora que o capacitor é preenchido com dois materiais diferentes cujas constantes dielétricas são κ 1 e κ 2 , respectivamente, na configuração mostrada na figura abaixo. Calcule a nova capacitância.

Passo 1

a) Vamos lembrar que a capacitância é dada por

C = ε 0 A d

Como as placas são quadradas e têm lado L , sua área vai ser

A = L ²

Substituindo na expressão da capacitância, temos que

C = ε 0 L ² d

Passo 2

b) Vamos tratar o capacitor da figura como dois capacitores em paralelo: o primeiro capacitor ( C 1 ) é formado por placas retangulares de lados L e 2 L / 3 e preenchido com um material de constante dielétrica κ 1 . O segundo capacitor ( C 2 ) é formado por placas retangulares de lados L e L / 3 e preenchido com material de constante dielétrica κ 2 .

Então vamos calcular suas capacitâncias:

C 1 = κ 1 ε 0 2 L 2 / 3 d = κ 1 ε 0 2 L 2 3 d

C 2 = κ 2 ε 0 L 2 / 3 d = κ 2 ε 0 L 2 3 d

Como C 1 e C 2 estão em série, a capacitância total vai ser a sua associação, dada por

C = C 1 + C 2

C = κ 1 ε 0 2 L 2 3 d + κ 2 ε 0 L 2 3 d

C = ( 2 κ 1 + κ 2 ) ε 0 L ² 3 d

Resposta

  1. C = ε 0 L ² d
  2. C = ( 2 κ 1 + κ 2 ) ε 0 L ² 3 d

Exercícios de Livros Relacionados

Na figura 25-96, V = 9,0 V, C 2 = 3,0 μF, C 4 = 4,0 μF e todos os capacitores estão inicialmente descarregados. Quando a chave S é fechada, uma carga total de 12 μC passa pelo ponto a e uma carga tota
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e
Um átomo de U 238 tem massa de 3,97 × 10 - 22 g . Calcule a taxa de decaimento radioativo de uma amostra de um grama daquele isótopo, cuja vida média é 6,45 × 10 9 anos.
Um frasco de perfume é aberto por um breve intervalo de tempo, liberando N moléculas no ar. Um minuto após serem liberadas, as moléculas de perfume apresentam uma dispersão dada por r r m s = 2,5c m .