Na Figura abaixo, e . A diferença de potencial aplicada é .
- Qual é a capacitância equivalente do circuito entre os pontos e ?
- Calcule a carga de cada capacitor e a diferença de potencial através de cada capacitor.
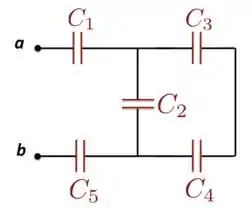
Passo 1
a) Vamos encontrar a resistência equivalente entre os capacitores e , que estão em série. Temos, então,
em que usamos o fato de que . Como está em paralelo com , a capacitância equivalente entre eles será:
em que usamos o fato de que . Dos valores dados no enunciado, a gente nota que podemos utilizar que e podemos simplificar para
Agora, está sem série com e , que são iguais. Portanto, teremos o seguinte:
em que, se utilizamos que , dá para gente que
Colocando os valores dados no enunciado, chegamos que capacitância equivalente entre os pontos e da Figura tem o seguinte valor
Passo 2
b) Para obtermos o valor da carga em cada capacitor, precisamos primeiro saber qual é a carga total do capacitor equivalente. Então
A carga dos capacitores , e , são iguais, já que eles estão em série. Tranquilo? Por isso, temos o seguinte
Agora, a diferença de potencial entre esses capacitores é diferente e, quando somadas, devem resultar em . Portanto,
Passo 3
b) Continuação...
Como e , podemos obter
Agora, essa é a diferença de potencial entre os terminais do capacitor . Por isso, a carga é
Por outro lado, e também temos a mesma diferença de potencial . Por isso, temos o seguinte
Portanto, como e estão em série, eles possuem a mesma carga
Resumindo, temos as seguintes cargas para cada um dos capacitors: