Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 13123456789101112141516171819202122232425

Enunciado

UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 9

Ache o centroide (centro de massa) da região R abaixo do gráfico de y = sin 2 ⁡ ( x ) no intervalo [ 0 , π 2 ]

Passo 1

Eaew, tudo certinho com você hoje?

Para começar esta questão vamos dar uma olhada em nossa região, beleza? Nós temos o seguinte:

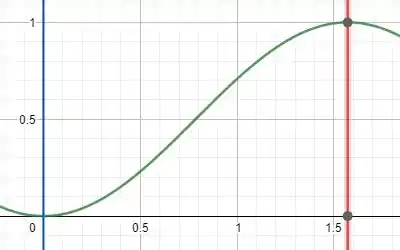
y = sin 2 ⁡ ( x ) e as linhas verticais azuis e vermelha, representam os limites x = 0 e x = π 2 , respectivamente! Ótimo! Para calcular as coordenadas do centroide é vamos utilizar as seguintes definições para sua coordenada:

x - = ∫ x ~ d A ∫ d A  

E também:

y - = ∫ y ~ d A ∫ d A

Em que x ~ e y ~ são as coordenadas do centro de massa de um retângulo infinitesimal de área d A , como na figura abaixo:

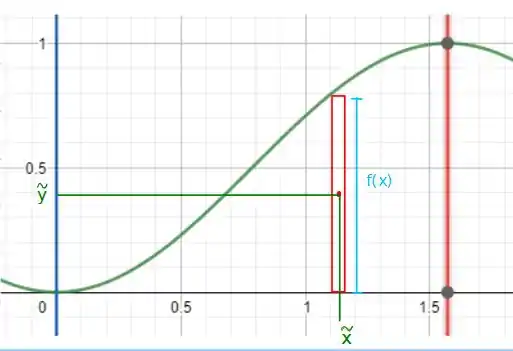
Ótimo! Com tudo isso podemos calcular as coordenadas de nosso centroide! Bora lá!

Passo 2

Vamos começar calculando:

∫ d A = ?

Já que este valor é comum a ambas as coordenadas! Mas quem é d A ? Ele é a área infinitesimal do retângulo montado acima, ou seja:

d A = f x d x = sin 2 ⁡ ( x ) d x

Considerando os limites de integração x = 0 e x = π / 2 , temos:

∫ 0 π / 2 sin 2 ⁡ ( x ) d x

Vamos resolver esta integral!

Passo 3

Temos o seguinte:

sin 2 ⁡ ( x ) = 1 2 1 - cos ⁡ 2 x

De forma que:

∫ 0 π / 2 sin 2 ⁡ ( x ) d x = 1 2 ∫ 0 π / 2 d x - 1 2 ∫ 0 π / 2 cos ⁡ ( 2 x ) d x

Agora precisamos relembrar as primitivas, e temos o nosso denominador! Bora lá!

Passo 4

Utilizando que:

1 2 ∫ 0 π / 2 d x = 1 2 x ​ 0 π / 2 = 1 2 π 2 - 0 = π 4

E que:

1 2 ∫ 0 π / 2 cos ⁡ ( 2 x ) d x = 1 2 1 2 sin ⁡ 2 x ​ 0 π 2 = 1 4 sin ⁡ π - sin ⁡ 0 = 0  

Portanto, temos que:

∫ d A = π 4         ( 1 )

Belezinha! Vamos calcular nossas coordenadas agora! Bora lá!

Passo 5

Começando com a coordenada x - , temos:

x - = ∫ 0 π / 2 x sin 2 ⁡ ( x ) d x π / 4           ( 2 )

Note que usei d A = sin 2 ⁡ ( x ) d x e que x ~ = x , pois neste caso eles podem ser identificados desta maneira, dá uma olhadinha na figura hehehehe! A integral no numerador requer integração por partes! Vamos fazer isso!

Passo 6

Escolhendo quem é nosso u d v , temos:

u = x → d u = d x

E também:

d v = sin 2 ⁡ x d x → v = ∫ sin 2 ⁡ x d x

Nós já resolvemos essa integral antes! Ela resulta em:

v = ∫ sin 2 ⁡ ( x ) d x = 1 2 ( x - 1 2 sin ⁡ 2 x )

Utilizando a fórmula da integração por partes, temos:

∫ u d v = u v ​ a b - ∫ a b v d u

∫ 0 π / 2 x sin 2 ⁡ ( x ) d x = 1 2 x x - 1 2 sin ⁡ 2 x ​ 0 π / 2 - 1 2 ∫ 0 π / 2 ( x - 1 2 sin ⁡ ( 2 x ) ) d x

Vamos expandir os termos e resolver esta integral que sobrou! Belezinha?

Passo 7

Começando expandindo alguns termos, temos:

π 4 π 2 - 1 2 sin ⁡ π - 0 - 1 2 ∫ 0 π 2 x d x + 1 4 ∫ 0 π 2 sin ⁡ 2 x d x = →

→ = π 2 8 - 1 2 x 2 2 ​ 0 π / 2 - 1 8 cos ⁡ 2 x ​ 0 π / 2

Em que usei:

∫ a b x n d x = x n + 1 n + 1 ​ a b

E também que:

∫ a b sin ⁡ ( c x ) d x = - cos ⁡ c x c ​ a b    

Temos então expandindo alguns termos e substituindo em (2), que:

x - = π 2 8 - π 2 16 + 1 8 + 1 8 π / 4 = π 2 + 4 4 π

Bora calcular o y - agora! Heheheheh!

Passo 8

O esquema é bem parecido, mas agora temos que:

y - = ∫ 0 π / 2 y sin 2 ⁡ ( x ) d x π / 4 = 1 2 ∫ 0 π / 2 sin 4 ⁡ ( x ) d x π / 4

Em que usei y ~ = f ( x ) / 2 , como pode dar uma olhadinha no esquema no passo 1. Para resolver esta integral no numerador vamos usar a seguinte identidade:

sin 2 ⁡ ( x ) = 1 2 1 - cos ⁡ ( 2 x )

Devagar a gente chega lá!

Passo 9

Temos que:

y - = 1 8 ∫ 0 π 2 1 - cos ⁡ 2 x 1 - cos ⁡ 2 x d x π 4

Vamos expandir alguns termos! Vai ficar da seguinte forma:

y - = 1 8 ∫ 0 π / 2 d x - 1 4 ∫ 0 π 2 cos ⁡ 2 x d x + 1 8 ∫ 0 π 2 cos 2 ⁡ ( 2 x ) d x π / 4

Para as duas primeiras integrais é necessário apenas identificar as primitivas, e para a terceira integral precisamos usar a relação:

cos 2 ⁡ ( 2 x ) = 1 2 1 + cos ⁡ ( 4 x )

De forma que temos que:

y - = 1 8 π 2 - 0 - 1 8 sin ⁡ π - sin ⁡ 0 + 1 16 ∫ 0 π 2 d x + 1 16 ∫ 0 π / 2 cos ⁡ ( 4 x ) d x π / 4

Novamente, identificando algumas primitivas temos:

y - = π 16 + 1 16 π 2 - 0 + 1 64 ( sin ⁡ 2 π - sin ⁡ ( 0 ) ) π / 4 = π 16 + π 32 π / 4 = 3 π 8 π = 3 8

Uff... acabou! A questão era isso! Te vejo na próxima! Tchauzinho!

Resposta

x - = π 2 + 4 4 π         e           y - = 3 8

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.