Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 12345678910111213141516171819202122232425

Enunciado

Encontre o centróide da região dentro da cardióide r = 1 + cos ⁡ θ .

Passo 1

A gente sabe calcular o centróide usando as relações:

x c = ∬ D   x   d A ∬ D   d A

y c = ∬ D   y   d A ∬ D   d A

Mas a região que nos foi dada está e coordenadas polares que, para nos lembrarmos, são:

x = r cos ⁡ θ           y = r sin ⁡ θ

Então, ná verdade, o que vamos calcular vai ser:

x c = ∬ D   r cos ⁡ θ   d A ∬ D   d A

y c = ∬ D   r sin ⁡ θ   d A ∬ D   d A

Então vamos tentar entender a região pra conseguir descrevê-la, que é só o que falta pra calcularmos as integrais!

Passo 2

Quando temos uma curva dessas complicadas com coordenadas polares, eu gosto sempre de tentar marcar uns pontos importantes pra tentar esboçar a curva mais ou menos, então vamos ver:

A curva começa com θ = 0 → r = 2 .

Para 0 ≤ θ ≤ π 2   → cos ⁡ θ decresce de 1 até 0 , então r decresce de 2 até 1 .

Para π 2 ≤ θ ≤ π   → cos ⁡ θ cresce em módulo de 0 até 1 , mas é negativo, então r decresce de 1 até 0 .

Para π ≤ θ ≤ 3 π 2   → cos ⁡ θ decresce em módulo de 1 até 0 , mas é negativo, então r cresce de 0 até 1 .

Para 3 π 2 ≤ θ ≤ 2 π   → cos ⁡ θ volta a ser positivo e cresce de 0 até 1 , então r cresce de 1 até 2 , fechando a curva.

Acho que assim já da pra ter uma boa noção de como fica a curva, mas se você quiser ver como que fica ela certinha, vamos ter algo assim:

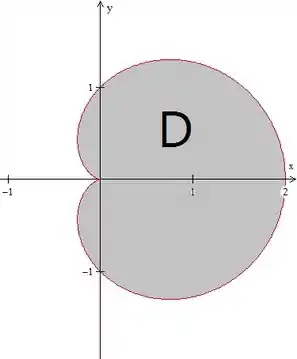
E a região D vai ser descrita por:

D = ( r , θ ) ∈ R 2 | 0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ 1 + cos ⁡ θ

Então agora sim podemos calcular tudo! Vamos começar com a integral do denominador que aparece nos dois termos, que é a mais simples.

Passo 3

Vamos ter:

∬ D   d A

Que, em coordenadas polares, vamos lembrar que:

d A = r   d r d θ

Então:

∬ D   d A = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r   d r d θ

⇒ ∫ 0 2 π r 2 2 │ 0 1 + cos ⁡ θ d θ

= 1 2 ∫ 0 2 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ   d θ

⇒ 1 2 θ │ 0 2 π + 2 sin ⁡ t │ 0 2 π + ∫ 0 2 π 1 + cos ⁡ 2 θ 2 d θ

= π + 1 4 θ │ 0 2 π + sin ⁡ 2 θ 8 │ 0 2 π = π + π 2

⇒ 3 π 2

Agora só falta as integrais dos numeradores, vamos ver como que é!

Passo 4

Vamos começar por x c :

x c = ∬ D   r cos ⁡ θ   d A ∬ D   d A

Então vamos calcular a integral:

∬ D   r cos ⁡ θ   d A

Que já temos a região descrita e tudo mais, então:

∬ D   r cos ⁡ t   d A = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r cos ⁡ θ ∙ r   d r d θ

⇒ ∫ 0 2 π cos ⁡ θ ∙ r 3 3 │ 0 1 + cos ⁡ θ d θ  

= 1 3 ∫ 0 2 π cos ⁡ θ 1 + cos ⁡ θ 3 d θ

= 1 3 ∫ 0 2 π cos ⁡ θ 1 + 3 ∙ cos ⁡ θ + 3 ∙ cos 2 ⁡ θ + cos 3 ⁡ θ d θ

= 1 3 ∫ 0 2 π cos ⁡ θ + 3 ∙ cos 2 ⁡ θ + 3 ∙ cos 3 ⁡ θ + cos 4 ⁡ θ d θ

Eita, que contas chatas... Vamos ver cada uma separado pra não ficarmos muito perdidos.

Passo 5

A primeira:

1 3 ∫ 0 2 π cos ⁡ θ d θ = sin ⁡ θ │ 0 2 π = 0

Passo 6

Depois:

1 3 ∫ 0 2 π 3 ∙ cos 2 ⁡ θ d θ = ∫ 0 2 π 1 + cos ⁡ 2 θ 2 d θ = 1 2 θ │ 0 2 π + sin ⁡ 2 θ 2 │ 0 2 π = π

Passo 7

Mais uma:

1 3 ∫ 0 2 π 3 ∙ cos 3 ⁡ θ d θ = ∫ 0 2 π 1 - sin 2 ⁡ θ cos ⁡ θ d θ

Que fazendo pela substituição:

u = sin ⁡ θ → d u = cos ⁡ θ d θ

∫ 1 - u 2   d u = u - u 3 3 = sin ⁡ θ │ 0 2 π - sin 3 ⁡ θ 3 │ 0 2 π = 0

Passo 8

E por último:

1 3 ∫ 0 2 π cos 4 ⁡ θ d θ = 1 3 ∫ 0 2 π 1 + cos ⁡ 2 θ 2 2 d θ = 1 12 ∫ 0 2 π 1 + 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ d θ

⇒ 1 12 θ │ 0 2 π + sin ⁡ 2 θ │ 0 2 π + ∫ 0 2 π 1 + cos ⁡ 4 θ 2 d θ

⇒ 1 12 2 π + θ 2 │ 0 2 π + sin ⁡ 4 θ 8 │ 0 2 π = 1 12 2 π + π = 3 π 12 = π 4

Ufa, quanta coisa... Mas vamos ver como que fica a soma toda.

Passo 9

Somando todas aqueles nossos resultados:

1 3 ∫ 0 2 π cos ⁡ θ + 3 ∙ cos 2 ⁡ θ + 3 ∙ cos 3 ⁡ θ + cos 4 ⁡ θ d θ = π + 0 + 0 + π 4

⇒ 5 π 4

Então, vamos ter que nossa coordenada x c vai ser:

x c = ∬ D   r cos ⁡ θ   d A ∬ D   d A

Vamos lembrar que ∬ D   d A = 3 π 2 , então:

x c = ∬ D   r cos ⁡ θ   d A ∬ D   d A = 5 π 4 ∙ 2 3 π = 5 6

Agora só falta a coordenada y c e, sinceramente, eu espero que seja bem mais fácil, que essa foi um saco, né? Mas vamos ver!

Passo 10

Vamos lembrar a fórmula que tinhamos lá em cima:

y c = ∬ D   r sin ⁡ θ   d A ∬ D   d A

Então só falta calcular:

∬ D   r sin ⁡ θ   d A = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r sin ⁡ θ ∙ r   d r d θ

⇒ ∫ 0 2 π sin ⁡ θ ∙ r 3 3 │ 0 1 + cos ⁡ θ d θ  

= 1 3 ∫ 0 2 π 1 + cos ⁡ θ 3 sin ⁡ θ d θ

Que dá pra resolver pela substituição:

u = 1 + cos ⁡ θ → d u = - sin ⁡ θ d θ

⇒ 1 3 ∫ 1 + cos ⁡ θ 3 sin ⁡ θ d θ = 1 3 ∫ u 3 - d u = - 1 3 ∙ u 4 4 = - 1 + cos ⁡ θ 4 12 │ 0 2 π

= - 1 12 1 + 1 4 - 1 + 1 4 = 0

Bem mais tranquilo, que sorte... haha

Mas ai vamos ver como fica o y c em si:

y c = ∬ D   r sin ⁡ θ   d A ∬ D   d A = 0 ∙ 2 3 π = 0

Pronto, agora sim!

Resposta

x c = 5 6

y c = 0

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.