Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 91234567810111213141516171819202122232425

Enunciado

  1. Calcule o centro de massa da lâmina D = x ,   y ∈ R 2 ; 4 x 2 + y 2 ≤ 1 ,   x ≥ 0 , se a densidade é proporcional à distância de x ,   y ao eixo y .

Passo 1

Então, a primeira coisa a se fazer em exercícios como esse é esboçar a sua região. Vamos lá?

Bem, primeiramente, a região D é formada pela inequação 4 x 2 + y 2 ≤ 1 . Mas... Se ao invés de pegarmos a inequação, olhássemos para a equação

4 x 2 + y 2 = 1

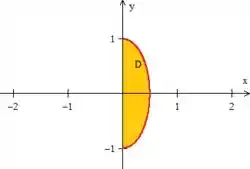
RARA! Essa equação nos representa uma... elipse centrada na origem:

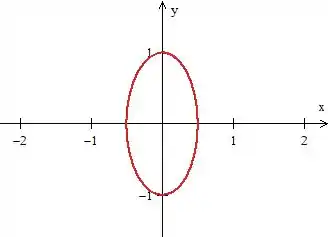
A inequação indica que estamos dentro dela

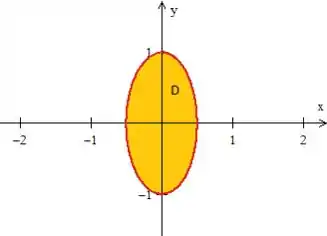
Mas calma! A região D também foi delimitada por x ≥ 0 , o que significa que estamos trabalhando apenas com o lado direito. Veja!

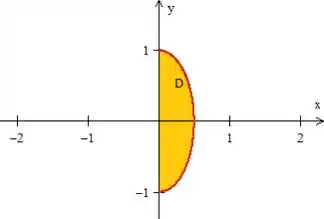
Passo 2

Muito bem! Para calcular a o centro de massa dessa coisa, devemos calcular antes três integrais extremamente importantes:

1 )     ∬ D y     ρ x ,   y d A

2 )     ∬ D x     ρ x ,   y d A

3 )     ∬ D ρ x ,   y d A

Agora, repare que em ambas devemos saber quem é essa função densidade ρ x ,   y , o que é muito fácil encontrar, afinal de conta ela é proporcional à distância d ao eixo x . Como a distância ao eixo x é

d = x

então

ρ x ,   y = k x

k é a constante que indica proporcionalidade, ok?

Bem, mas não é só a função de densidade que devemos conhecer...

Passo 3

Precisamos saber também a respeito desse sólido D aí!

Ora! Já conhecemos quem é o sólido, mas precisamos descrevê-lo para podermos trabalhar.

Como estamos trabalhando com uma elipse... Podemos pensar em uma parametrização elíptica, onde devemos comparar

4 x 2 + y 2 = 1     →           2 x 2 + y 2 = 1

com a equação fundamental da trigonometria

cos 2 ⁡ θ + sin 2 ⁡ θ = 1

onde podemos falar que

x = 1 2 r cos ⁡ θ

e

y = r sin ⁡ θ

O Jacobiano desse tipo de mudança é o produto dos números que estão atrás desses caras pelo r ...

J = 1 2 ∙ 1 ∙ r

sacou?

Passo 4

Agora se lembre, não podemos terminar uma mudança sem antes sabermos onde estão variando os novos caras, no caso, r e θ :

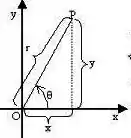
Por comparação com

podemos ver que θ dá uma meia volta, mas começando 90 ° antes

- π 2 ≤ θ ≤ π 2

enquanto que o r varia da origem até a curva vermelha

0 ≤ r ≤ c u r v a   v e r m e l h a

como a curva vermelha é

4 x 2 + y 2 = 1

substituindo as coordenadas...

4 1 2 r cos ⁡ θ 2 + r sin ⁡ θ 2 = 1

e simplificando um pouco encontramos...

4 ∙ 1 4 r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ = 1

r 2 cos 2 ⁡ θ + sin 2 ⁡ θ = 1

r = 1

que r máximo é 1

0 ≤ r ≤ c u r v a   v e r m e l h a

0 ≤ r ≤ 1

Passo 5

Retornando à primeira integral que devemos resolver...

1 )     ∬ D y     ρ x ,   y d A

e substituindo...

∫ - π 2 π 2 ∫ 0 1 r sin ⁡ θ ∙ 1 2 r cos ⁡ θ ∙ J   d r d θ =

∫ - π 2 π 2 ∫ 0 1 r 3 sin ⁡ θ ∙ 1 2 cos ⁡ θ ∙   d r d θ

integrando separadamente r , esses senos e cossenos viram constantes...

1 2 ∫ - π 2 π 2 sin ⁡ θ ∙ cos ⁡ θ ∫ 0 1 r 3   d r d θ

Pow! Concorda que essa integral de dentro é um número?

Então ela vaza da integral de fora (isso acontece sempre quando não tem variáveis nos intervalos)

1 2 ∫ 0 1 r 3   d r ∙ ∫ - π 2 π 2 sin ⁡ θ ∙ cos ⁡ θ d θ

Cara, um super bizu que eu vou te dar aqui agora é que quando tivermos integral de seno vezes cosseno em um intervalo simétrico como é o caso, - π 2 , π 2 , o resultado da integral é z e r o

1 2 ∫ 0 1 r 3   d r ∙ ∫ - π 2 π 2 sin ⁡ θ ∙ cos ⁡ θ d θ = 1 2 ∫ 0 1 r 3   d r ∙ 0

∬ D y     ρ x ,   y d A = 0

Passo 6

Quanto à outra integral...

2 )     ∬ D x     ρ x ,   y d A

Repetindo o processo

∫ - π 2 π 2 ∫ 0 1 1 2 r cos ⁡ θ 1 2 r cos ⁡ θ r   d r d θ =

∫ - π 2 π 2 ∫ 0 1 1 4 r 3 cos 2 ⁡ θ d r d θ

resolvendo a integral de dentro

∫ - π 2 π 2 ∫ 0 1 1 4 r 3 cos 2 ⁡ θ d r d θ =

1 4 ∫ - π 2 π 2 cos 2 ⁡ θ ∫ 0 1 r 3 d r d θ =

1 4 ∫ - π 2 π 2 cos 2 ⁡ θ r 4 4 0 1 d θ =

1 4 1 4 ∫ - π 2 π 2 cos 2 ⁡ θ d θ

Para essa integral, preciso que você se recorde que

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

logo

1 4 1 4 ∫ - π 2 π 2 cos 2 ⁡ θ d θ = 1 16 ∫ - π 2 π 2 1 2 + cos ⁡ 2 θ 2 d θ

1 16 1 2 θ + 1 2 sin ⁡ 2 θ 2 - π 2 π 2 = 1 16 1 2 π 2 - 1 2 - π 2   =

π 32

Passo 7

Calma! Não se estressa! Mas temos mais uma integral a se resolver...

∬ D ρ x ,   y d A =

Basta substituir e resolver tuuuudo novamente como segue

∫ - π 2 π 2 ∫ 0 1 1 2 r cos ⁡ θ   r d r d θ =

∫ - π 2 π 2 ∫ 0 1 1 2 r 2 cos ⁡ θ   d r d θ =

1 2 ∫ - π 2 π 2 cos ⁡ θ ∫ 0 1 r 2   d r d θ =

1 2 ∫ - π 2 π 2 cos ⁡ θ r 3 3 0 1 d θ =

1 2 1 3 ∫ - π 2 π 2 cos ⁡ θ d θ =

1 6 sin ⁡ θ - π 2 π 2 = 1 6 sin ⁡ π 2 - sin ⁡ - π 2 =

1 3

Passo 8

Agora basta substituir nas fórmulas do centro de massa, ou seja:

x - = ∬ D x     ρ x ,   y d A ∬ D ρ x ,   y d A

y - = ∬ D y     ρ x ,   y d A ∬ D ρ x ,   y d A

onde vamos obter

x - = π 32 1 3 = 3 π 32

y - = 0 1 3 = 0

Resposta

3 π 32 ,   0

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.