Lista de exercícios 9 – UFABC – Técnicas de integração– questão 20 item b
Encontre o centroide das seguintes regiões:
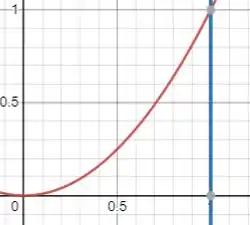
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
O centroide é a coordenada do centro geométrico um objeto.
O centroide é dado por:
Para y a função deve ser inversa
Veja como que a Area é bastante importante, pois ela aparece e também o seu valor infinitesimal. Bom a área é dada por:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, a área é:
E como dado, , então
Passo 3
Já que conseguimos a área, então podemos obter as coordenadas do nosso centroide.
Para a coordenadas x:
E para a coordenada y:
Já que então
Assim o centroide fica no ponto:
Resposta
Exercícios de Livros Relacionados
(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.