Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 10123456789111213141516171819202122232425

Enunciado

  1. Calcule as coordenadas x - ,   y - do centro de massa de uma chapa homogênea D com o formato de um triângulo isósceles com base 10 c m e altura 5 c m .

Passo 1

Pow! A primeira coisa a se fazer aqui é sem dúvidas enxergar esse triângulo. Como ele é isósceles, possui um uma base e duas outras arestas sendo a mesma:

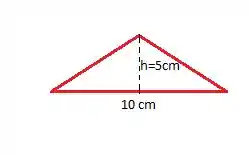
Colocando esse triângulo no plano cartesiano (para facilitar as contas, vamos coloca-lo com o vértice esquerdo na origem):

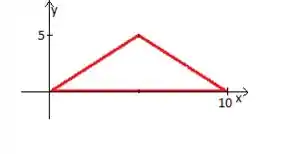
Bem, para encontrar o centro de massa desse cara, basta que apliquemos a fórmula:

C M = x - ,   y -

onde x - e y - são

x - = ∬ D x     ρ x ,   y d A ∬ D ρ x ,   y d A

e

y - = ∬ D y     ρ x ,   y d A ∬ D ρ x ,   y d A

Esse ρ x ,   y é a densidade da região, mas como essa região é homogênea, a função de densidade é uma constante k , logo podemos eliminá-la das integrais:

x - = k   ∬ D x     d A k ∬ D   d A

e

y - = k   ∬ D y     d A k   ∬ D   d A

cortando esses K s e lembrando que ∬ D   d A é a área da região D , teremos que calcular afinal..

x - = ∬ D x     d A Á r e a   ( D )

e

y - = ∬ D y     d A Á r e a   D

Passo 2

Como em ambas as equações nós temos que encontrar o valor da área da região D , calculemos:

Á r e a   D = Á r e a   d o   t r i â n g u l o

Á r e a   D = B a s e ∙ A l t u r a 2

logo

Á r e a   D = 10 ∙ 5 2 = 25   c m 2

Passo 3

Outra coisa que temos em ambas coordenadas são aquelas integrais duplas que necessitamos de descrever a região D , o triângulo.

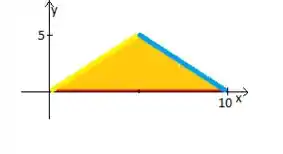
Podemos nesse caso descrevê-lo como o T I P O   2 , afinal temos que y varia em um intervalo numérico bem definido

0 ≤ y ≤ 5

Enquanto que o x varia da reta amarela até a azul (acompanhe a reta preta com o dedo para você ver isso experimentalmente ):

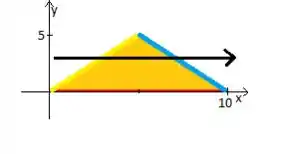
Resta-nos saber quem é a essas retas amarela e azul. Bora?

Passo 4

Beleza, a reta amarela vai da origem até o ponto 5 ,   5 , pois a metade da base é 5 e a altura também.

Portanto a única reta que passa pela origem e tem as coordenadas iguais é justamente essa reta

y = x

Agora, enquanto a reta azul, preciso que recorde de como encontrar uma reta om dois pontos, afinal ela sai do ponto 5 ,   5 , mas chega ao ponto 0 ,   10 . Então o ∆ y é

∆ y = 10 - 5 = 5

e ∆ x = 0 - 5 = - 5

colocando na forma geral de reta

y - y 0 = ∆ y ∆ x x - x 0

substituindo ( x 0 ,   y 0 ) pela coordenada do pondo de chegada, ou seja

( x 0 ,   y 0 ) = 0 ,   10

y - 10 = 5 - 5 x                 ⇒ a r r u m a n d o   d e   u m a   f o r m a   m a i s b e l a

x = - y + 10

onde podemos concluir que

r e t a   a m a r e l a ≤ x ≤ r e t a   a z u l

y ≤ x ≤ - y + 10

Passo 5

Substituindo então na primeira integral da coordenada x - do centro de massa:

x - = ∬ D x     d A Á r e a   ( D )

Vamos obter

∫ 0 5 ∫ y - y + 10 x d x d y =

Calculando a integral de dentro primeiro...

∫ 0 5 ∫ y - y + 10 x d x d y = ∫ 0 5 x 2 2 y - y + 10 d y =

substituindo os valores em x ...

∫ 0 5 - y + 10 2 2 - y 2 2 d y

simplificando um pouco eliminando os parênteses...

∫ 0 5 y 2 - 20 y + 100 2 - y 2 2 d y =

∫ 0 5 y 2 2 - 10 y + 50 - y 2 2 d y = ∫ 0 5 - 10 y + 50   d y

integrando em y

∫ 0 5 - 10 y + 50   d y = - 10 y 2 2 + 50 y 0 5 =

- 5 5 2 + 50 ∙ 5 = 5 2 ∙ 10 - 5 3

Dividindo o resultado pela área...

x - = ∬ D x     d A Á r e a   ( D ) = 5 2 ∙ 10 - 5 3 5 2 = 5

Passo 6

Para a o y - vamos repetir o processo, mas dessa vez resolvendo

∫ 0 5 ∫ y - y + 10 y d x d y =

∫ 0 5 ∫ y - y + 10 y d x d y =

Como y é considerado constante perto de d x

∫ 0 5 y ∫ y - y + 10 d x d y =

∫ 0 5 y x y - y + 10 d y =

Substituindo os limites e terminando a integral vamos obter:

∫ 0 5 y - y + 10 - y d y = ∫ 0 5 - 2 y 2 + 10 y   d y =

- 2 y 3 3 + 10 y 2 2 0 5 = - 2 y 3 3 + 5 y 2 0 5 =

- 2 3 5 3 + 5 3 = 5 3 3

Dividindo o resultado pela a área

y - = ∬ D y     d A Á r e a   D = 5 3 3 25

= 5 3

Resposta

O centro de massa situa-se a 5 3 c m da base, sobre sua mediatriz

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.