Calcule a massa e o centro do massa da lâmina que ocupa a região triangular no plano delimitada pelas retas , e com densidade .
Lembre que a massa e o centro de massa de uma lâmina que ocupa uma região no plano são dados por
Passo 1
Bem, aqui vamos ter que calcular três integrais, uma para a massa e mais duas para as coordenadas do centro de massa, mas o enunciado mesmo já dá as fórmulas, então vamos só aplicá-las.
Mas antes de tudo, vamos desenhar as retas para entendermos melhor a região e sabermos os limites da integral certinho:
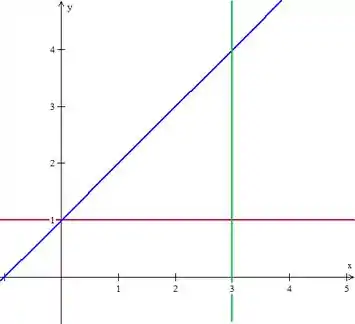
Que é esse triângulo aí, que é uma região do tipo e do tipo , mas que eu vou usar do tipo só porque é o mais comum, tá?
Então ficamos com e de limites e agora vamos lá começar a calcular nossas integrais!
Passo 2
Vamos começar com a massa, que a gente tinha a fórmula:
Tranquilinho, até, né? Vamos ver se damos sorte com as próximas!
Passo 3
Agora vamos ver a coordenada do centro de massa:
Que a gente até já tem a massa, então ficamos com:
Também nada muito bizarro... E só falta uma agora, estamos quase lá!
Passo 4
Finalmente, vamos ver a coordenada :
E vamos substituir tudo:
Essa teve umas continhas mais chatas, mas nada que a gente não soube resolver também.