Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Regiões Planas

Ver Teoria
Exercício 21345678910111213141516171819202122232425

Enunciado

Encontre o centróide da região no primeiro quadrante limitada pelo eixo x , pela parábola y 2 = 2 x e pela reta x + y = 4 .

Passo 1

Na teoria, a gente viu qe o centróide de uma região plana pode ser encontrado utilizado as fómulas:

x c = ∬ D   x   d A ∬ D   d A

y c = ∬ D   y   d A ∬ D   d A

Então, na verdade, o que nós temos mesmo que cálcular são essas três integrais aí, né?

Vamos ver com fica cada uma delas!

Passo 2

Vamos começar pela integral mais simples, que aparece no denominador das duas fórmulas:

∬ D   d A

A nossa região D é limitada pelas curvas: y 2 = 2 x , x + y = 4 e o eixo x , então vamos esboçar mais ou menos como que ela vai ficar:

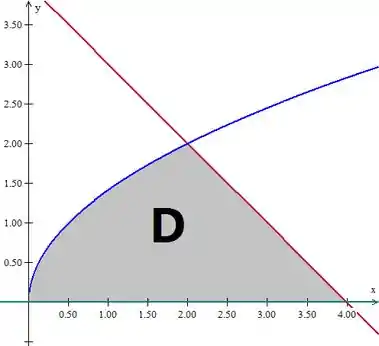
Aqui podemos ver que temos uma região do tipo 2 , com y variando entre 0 e aquele ponto de interseção, que se dá em:

y 2 2 = 4 - y → y 2 + 2 y - 8

⇒ y 1 = - 4         y 2 = 2

Então nossa região vai ser descrita por:

D = ( x , y ) ∈ R 2 | 0 ≤ y ≤ 2 , y 2 2 ≤ x ≤ 4 - y

Passo 3

Agora calculando mesmo a integral, vamos ter:

∬ D   d A = ∫ 0 2 ∫ y 2 2 4 - y d x d y

⇒ ∫ 0 2 x │ y 2 2 4 - y d y = ∫ 0 2 4 - y - y 2 2 d y

= 4 y │ 0 2 - y 2 2 │ 0 2 - y 3 6 │ 0 2 = 8 - 2 - 4 3

= 6 - 4 3 = 18 - 4 3 = 14 3

Agora só falta calcular as integrais dos numeradores. Vamos lá!

Passo 4

Vamos começar pela do x , lembrando da fórmula:

x c = ∬ D   x   d A ∬ D   d A

Então o que nós queremos calcular é:

∬ D   x   d A

Mas já descrevemos a região, então podemos fazer:

∬ D   x   d A = ∫ 0 2 ∫ y 2 2 4 - y x   d x d y

⇒ ∫ 0 2 x 2 2 │ y 2 2 4 - y d y = 1 2 ∫ 0 2 16 - 8 y + y 2 - y 4 4 d y

= 1 2 16 y │ 0 2 - 4 y 2 │ 0 2 + y 3 3 │ 0 2 - y 5 20 │ 0 2

⇒ 16 - 8 + 4 3 - 4 5

= 16 ∙ 15 - 8 ∙ 15 + 4 ∙ 5 - 4 ∙ 3 15 = 128 15

Então, substituindo:

x c = ∬ D   x   d A ∬ D   d A = 128 15 ∙ 3 14 = 384 210 = 64 35

Passo 5

Agora vamos fazer a mesma coisa para y c :

∬ D   y   d A = ∫ 0 2 ∫ y 2 2 4 - y y   d x d y

⇒ ∫ 0 2 y 4 - y - y 2 2 d y = ∫ 0 2 4 y - y 2 - y 3 2 d y

⇒ 2 y 2 │ 0 2 - y 3 3 │ 0 2 - y 4 8 │ 0 2

= 8 - 8 3 - 2 = 6 - 8 3 = 18 - 8 3

= 10 3

E vamos substituir de novo:

y c = ∬ D   y   d A ∬ D   d A = 10 3 ∙ 3 14 = 10 14 = 5 7

Pronto, tudo feito!

Resposta

x c = 64 35

y c = 5 7

Exercícios de Livros Relacionados

(a) Verifique que f x ,y = 4 x y , s e0 ≤ x ≤ 1,0 ≤ y ≤ 1 0 , c a s oc o n t r á r i o á é uma função densidade conjunta.(b) Se X e Y são variáveis aleatórias cuja função densidade conjunta é f da par
Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ . D é uma região triangular com vértices 0 ,0 ,2 ,1 ,0 ,3 ; ρ x ,y = x + y
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento a , se a densidade em qualquer ponto for proporcional ao quadrado da sua distâ
Xavier e Yolanda têm aulas que terminam ao meio-dia e concordaram em se encontrar todo dia depois das aulas. Eles chegam em um café separadamente. O tempo de chegada de Xavier é X e o da Yolanda é Y ,
Encontre o centro de massa da lâmina do Exercício 13 se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.