Lista de exercícios 10 – UFABC – Técnicas de integração– questão 21 item c
Encontre a massa e o centroide das lâminas abaixo:
c) A lâmina delimitada pelo eixo , e a curva e de densidade
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Nessa questão, temos uma curva representada pela função:
A região abaixo dessa curva, e acima do eixo é justamente o que o enunciado chama de lâmina, que tem densidade .
Dada a função:
Desenhando no gráfico (lembrando que a curva é uma parábola virada para baixo), nossa lâmina é essa região em preto 😊
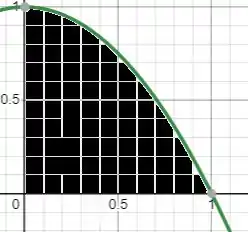
O nosso objetivo é calcular a massa e o centroide dessa lâmina!
Mas, você tá lembrado como calculamos o centroide de uma região?
Essa é a área.
A parte mais importante é sabermos usar a função recebida para montarmos gráfico, por quê?
Sabemos que a densidade é a massa dividido pela área, ou seja:
De forma que:
E ainda o centroide:
Para a função deve ser inversa
Veja como que a Area é bastante importante. Bom a área é dada por:
Onde é a função dada. Viu como a área é importante?! Bom ... Vamos lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Façamos antes a área:
O que são os limites a e b? Vamos ver?!
São os limites onde a integração de x existe. Bom, podemos achar isso vendo quando que o x cruza o eixo x, ou seja y=0
Pegando somete a parte positiva :
Sabendo que
Passo 3
A massa é então:
Para as coordenadas do centroide:
Para a coordenada x do centroide:
Para a coordenada y:
ANTES, devemos achar a função , assim:
Façamos de forma que . E quando fazemos uma substituição, qualquer que seja, devemos também levar o limite, assim:
Podemos melhorar esse monstrinho, né?!
Assim o centroide é:
E o centroide fica posicionado dessa forma na imagem da função:
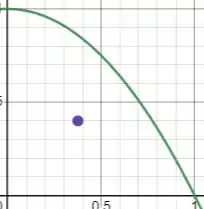
Resposta
A massa:
E o centroide: