Lista de exercícios 9 – UFABC – Técnicas de integração– questão questão 20 item c
Encontre o centroide das seguintes regiões:
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
O centroide é a coordenada do centro geométrico um objeto.
O centroide é dado por:
Para y a função deve ser inversa
Veja como que a Area é bastante importante, pois ela aparece e também o seu valor infinitesimal. Bom a área é dada por:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, a área é:
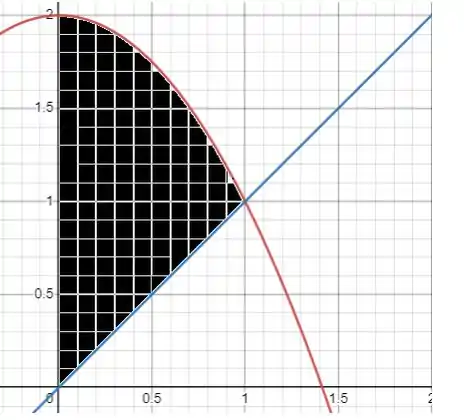
Primeiro para facilitar precisamos saber quais são os limites de integração. Como podemos ver na imagem, vai de 0 até ponto onde as funções são iguais, então vamos achar ode que as funções se igualam:
Passando tudo pro mesmo lado:
Aplicando bhaskara:
Como no gráfico nos importa somente o valor positivo, logo:
Logo os limites de integração vão de 0 até 1. Assim podemos achar nossa área, sabendo que a função f(x) é a função superior menos a inferior:
E como dado, , então
Passo 3
Já que conseguimos a área, então podemos obter as coordenadas do nosso centroide.
Para a coordenadas x:
E para a coordenada y:
Já que então , de forma que
Primeiro vamos resolver a integral? Fica mais fácil, não acha?! Então seja:
Façamos um substituição:
De forma que:
E:
Lembre-se que quando fazemos uma substituição, qualquer que seja, temos que verificar como são os limites nessa transformação, assim:
Assim a nossa nova integral fica:
Existe uma propriedade importante das integrais, que é:
Ou seja, podemos trocar os limites de integração de ordem, considerando que a volta seria parte negativa.
Assim podemos fazer:
Que é também:
Podemos simplificar isso:
Resumindo:
Achamos o valor da nossa integral, assim podemos retornar à:
Assim são as coordenadas do centroide:
E assim centroide fica na região:
