Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 271234567891011121314151617181920212223242526

Enunciado

Uma bala de massa m se movendo na horizontal com velocidade v atinge e gruda na borda de uma roda de massa M e raio R, fixa em um eixo passando pelo seu centro e livre para rodar. A velocidade angular final ω f da roda é:

a)   ω f = 2 R m + M v

b) ω f = v R 1 1 + M 2 m

c)   ω f = v R 1 1 + m 2 M

d) ω f = m R v 1 + M 2 m

e) Nenhuma das anteriores

Passo 1

Beleza, temos aqui um caso de colisão inelástica (os dois corpos sae grudados!), sendo que é uma colisão com rotação.

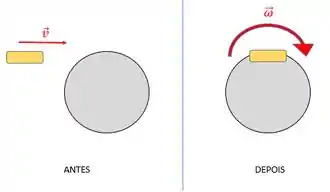
A gente lembra lá da colisão que o momento se conserva, né. Aqui, vai ser a mesma coisa, só que como temos uma rotação aqui, vamos conservar o momento angular.

L i = L f

Sendo que inicialmente, teremos o momento da bala, que é uma partícula, e no final, teremos o momento do sistema roda+bala, que é um corpo rígido.

m v R = I ω

m v R = m R 2 + M R 2 2 ω

Agora é só brincar de matemática e deixar a velocidade angular final em evidência.

2 m v = 2 m R + M R ω

2 m v = R 2 m + M ω

ω = v R 2 m 2 m + M

ω = v R ( 1 1 + M 2 m )

Resposta

Letra b)

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .