Um haltere composto por uma barra delgada de massa desprezível e comprimento L possui em cada extremidade um pequeno corpo de massa de tamanho desprezível. O haltere é colocado para girar sem atrito em torno de um eixo horizontal perpendicular à barra, que passa por um ponto localizado a do seu comprimento. O haltere é abandonado no repouso na posição horizontal (ver desenho). Expresse suas respostas em função de e da aceleração gravitacional .
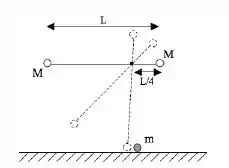
- Calcule o momento de inércia do haltere em relação àquele eixo de rotação.
- Calcule a velocidade linear da extremidade mais comprida do haltere quando ela atinge a posição inferior.
- Se, nesta posição inferior, o haltere colidir com um outro corpo de massa e tamanho também desprezível, inicialmente em repouso e que fica grudado no haltere, qual será a velocidade angular do conjunto logo depois da colisão?
Passo 1
a)
Vamos dar uma olhada numa figura melhor, haha.
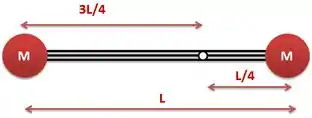
Para calcular o momento de inércia do haltere em relação a esse ponto basta somar o momento de inércia dos dois pesos de massa M.
Passo 2
Como o momento de inérica de uma partícula pontual é dado por: , a gente vai ter:
Daí, temos que . Substituindo...
Passo 3
b)
Pra simplificar as contas, vamos fazer uma mudança de refencial de “solo”. Ao invés de considerar o solo onde o desenho da questão mostrou vamos considerar na reta horizontal que passa pelo eixo de rotação.
Depois que o haltere girar a gente vai ter :
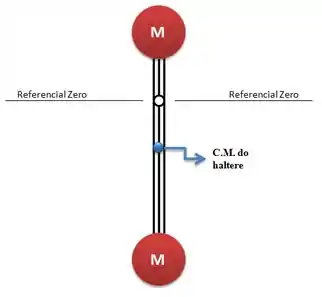
Fazendo a conservação de energia mecânica, teremos:
No caso lá da figura 1 é fácil de ver que , né?
Tanto a energia cinética vai ser zero, pois eles sairão do repouso, quanto o potencial também, pois como a barra toda vai estar no nosso referencial zero, o da formulinha será zero.
Passo 4
Daí só vai restar...
Nesse caso, nossa vai ser justamente a soma da energia potencial com a energia cinética de rotação do haltere.
Ah, vale lembrar que o ponto em que a gente vai calcular a energia potencial é o centro de massa do haltere que se localiza exatamente no meio da barra. Assim, vamos ter:
Como e ...
Isolando o , a gente vai ter:
Passo 5
Mas ele pediu a velocidade linear da bola que está mais embaixo, que a gente calcula por :
Nosso raio será . Finalmente substitundo o que a gente achou...
Passo 6
c)
Beleza, a gente sabe que vai ter uma força . Mas quando o haltere está na vertical a força vai estar na mesma linha de atuação do eixo de rotação. Saca só!
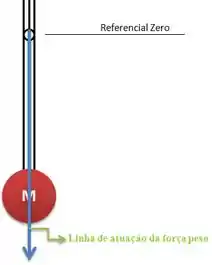
Dessa forma o torque nesse ponto é nulo e a gente vai poder calcular usando conservação do momento angular. :D~
A parte inicial a gente já sabe, e é simples de calcular, só substituir o que a gente já calculou na a e b.
O nosso vai mudar um pouco, mas também é tranquilo de calcular. É só somar o momento de inércia do corpo que vai ser colidido com o haltere.