Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 812345679101112131415161718192021222324252627

Enunciado

Momento angular

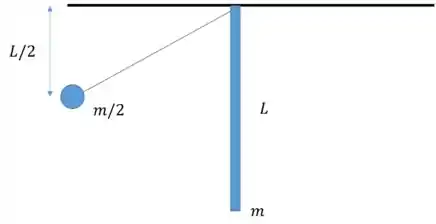
Dois pêndulos estão pendurados no mesmo ponto. Um deles é composto por uma corda de comprimento L e massa desprezível e um corpo puntiforme de massa M / 2 preso à extremidade da corda. O outro pêndulo é composto por uma haste homogênea também de comprimento L e massa M . O pêndulo formado pela corda e a massa pontual éafastado do equilíbrio até uma altura L / 2 e liberado de modo a colidir com o outro pêndulo ao atingir a posição vertical. Considerando as leis de conservação relevantes do problema e supondo que o corpo puntiforme fica em repouso após a colisão, a velocidade angular da haste, após a colisão, vale:

  1. 3 / 2 g / L 1 2
  2. 1 / 2 g / L 1 2
  3. 8 / 5 g / L 1 2
  4. 5 / 2 g / L 1 2
  5. Nenhuma das outras alternativas.

Momento de inércia de uma barra:

I C M = M L 2 12

Passo 1

Este problema, apesar de não parecer, é um problema de conservação do momento angular, saca só:

Passo 2

Começando com uma conservação de energia mecânica da massa, descobrimos a velocidade que a massa está quando o pêndulo dela fica na vertical:

E i = E f

No início a massa está parada logo a sua energia será só potencial gravitacional

E i = M 2 g L 2 = M g L 4

Onde definimos como nível de referência a altura da massa quando o fio estiver totalmente vertical

Quando o fio estiver totalmente vertical a sua energia mecânica será puramente cinética

E f = M 2 v 2 2 = M v 2 4

Igualando essas energias

E i = E f → M g L 4 = M v 2 4 → v 2 = g L

v = g L

Passo 3

Quando o pêndulo chega na vertical e colide com a barra o momento angular é conservado, já que não há torque externo:

L i = L f

Antes da colisão o momento angular é somente o da massinha pois a barra está em repouso! Como a velocidade da barra é perpendicular ao raio da sua trajetória

L i = M 2 v L

Como já calculamos a velocidade no passo anterior

L i = M 2 g L L

Passo 4

Após a colisão a massinha fica parada e quem começa a rotacionar é a barra, assim o nosso momento angular final fica

L f = I ω

O momento de inércia que entra aqui é o momento em relação à ponta superior da barra, só que o enunciado nos deu o momento de inércia em relação ao centro de massa! Pra calcular I basta usar o teorema dos eixos paralelos!

I = I C M + M d 2

Esse d é a distância do centro de massa em relação ao eixo de rotação. No nosso caso d = L / 2 . Assim

I = I C M + M L 2 2 = M L 2 12 + M L 2 4

I = M L 2 3

Assim o nosso momento angular final fica

L f = M L 2 3 ω

Passo 5

Usando a conservação de momento angular

L i = L f

M 2 g L L = M L 2 3 ω

Cortando M L dos dois lados e isolando o ω

ω = 3 2 g L L = 3 2   g L L 2

ω = 3 2 g L

Olhando as opções a resposta vai ser a letra A

Resposta

Letra A

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .