Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 912345678101112131415161718192021222324252627

Enunciado

Momento Angular

Uma porta, de largura 0,8 m e momento de inércia (em relação ao eixo das dobradiças) de 4 kg.m², está em repouso e aberta fazendo um ângulo de 90° em relação à parede. Um projétil de massa 5 g é disparado com velocidade de 300 m/s perpendicularmente à porta (a massa do projétil em relação a porta pode ser desprezada). Após o choque, o projétil fica encravado na beirada da porta. Qual é o intervalo de tempo entre o choque do projétil

com a porta e o instante em que a porta se fecha (encosta nos batentes da parede)?

a)   t   =   π / 0 ,   6   s

b)   t   =   π / 7   s

c)   t   =   π / 5   s

d) t   =   π / 600   s

e) t   =   π / 0 ,   5   s

Passo 1

Temos a situação em que a bala se choca com a beirada da porta, como na figurinha abaixo:

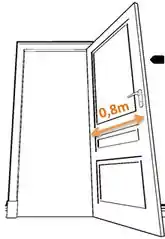
Além disso, temos os seguinte dados:

d = 0,8 m

I p = 4 k g . m 2

θ = 90 ° = π 2 r a d

m = 5 g

v = 300 m / s

Bora lá!

Passo 2

Como não existe nenhum torque resultante no sistema o momento angular se conserva, logo a gente pode escrever:

L p o r t a i + L b a l a i = L c o n j u n t o

I p ω p + m v d = I c o n j u n t o . ω

Mas daí, como a porta estava parada no início ω p = 0 e daí teremos:

m v d = I c o n j u n t o . ω

Passo 3

Como o I c o n j u n t o aumentou em relação à I p , podemos escrever que:

I c o n j u n t o = I p + I b a l a = I p + M d ²

Além disso, nosso ω pode ser substituído por θ ∆ t . Daí, substituindo na equação do Passo 2...

m v d = [ I p + M d 2 ] θ ∆ t

Passo 4

Isolando quem nós queremos, o ∆ t , teremos:

∆ t = I p + M d 2 θ m v d

Substituindo os valores:

∆ t =   [ 4 + 0,005.0,64 ] π 2 0,005.300.0,8 = 1,668 π = π 0,6 s

Resposta

Letra A

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .