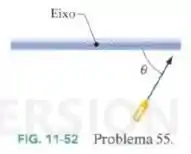
Uma barra fina uniforme com de comprimento e massa pode girar em um plano horizontal em torno de um eixo vertical passando pelo centro. A barra está em repouso quando uma bala de é disparada, no plano de rotação, em direção a uma das suas extremidades. Vista de cima, a trajetória da bala faz um ângulo de com a haste (Fig. 11-52). Se a bala se aloja na barra e a velocidade angular da barra é imediatamente após a colisão, qual é a velocidade da bala imediatamente antes do impacto?
Passo 1
Se analisarmos o sistema como um todo, vemos que não há torque externo agindo no mesmo, portanto, podemos usar a conservação do momento angular!
Como a barra está em repouso antes do impacto, o momento angular inicial se dá somente pelo movimento da bala:
Substituindo os valores:
Passo 2
Após o impacto nós temos uma barra com uma bala acoplada girando com velocidade angular .
Para encontrar o momento de inércia do sistema:
E o momento angular do sistema após o impacto é dado por:
Passo 3
Agora é só igualar os momentos angulares antes e depois do impacto!