Enunciado das questões (Q4) e (Q5).
O sistema representado ao lado, formado por duas partículas de massas e , ligadas por uma haste em forma de gancho, de massa desprezível e comprimento , pode deslizar sem atrito sobre o plano horizontal . Uma terceira partícula, de massa , movendo-se sobre o plano com velocidade , colide com o sistema formado pelas partículas e , inicialmente parado, ficando presa no gancho.
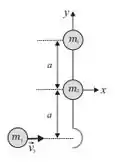
(Q5) [1,0 ponto] Depois da colisão a velocidade angular de rotação do sistema em torno do seu centro de massa é:
Passo 1
Bem, esse problema parece ser bem complicado, neh? Para facilitar, vamos começa-lo explicitando o que vamos fazer para encontrar a velocidade angular , ta legal?
Na teoria, quando temos um corpo girando, podemos associar recuperar a velocidade angular de rotação desse corpo através do momento angular ...
Então, se queremos o memento angular nesse problema, podemos sair em busca do momento angular e do momento de inércia e depois... Bem... Depois é só substituir:
Capiche? Bora lá então!
Passo 2
Primeiro, vamos encontrar o momento angular! Beleza?
De acordo com a teoria, o se não a intromissão de nenhuma força externa no sistema, então o momento angular também se conserva o que significa que o momento angular antes da colisão é o mesmo momento angular depois da colisão (o cara que nós usaremos para encontrar ):
Pow! O momento angular do sistema de partículas antes da colisão, podemos encontrar também pela definição:
Onde é a distância da partícula que está em movimento antes da colisão () com o centro de massa da haste...
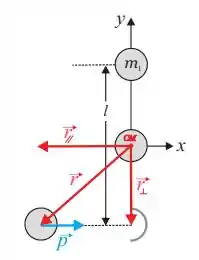
POW! A álgebra nos garante que o módulo do produto vetorial , portanto o módulo do momento angular pode ser dado por...
Onde é o módulo de e é o módulo de . O ângulo é o ângulo entre e :
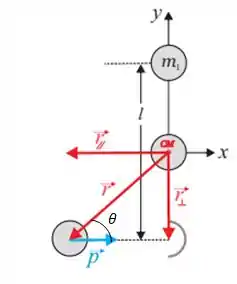
Então, por trigonometria...
Considerando que ...
Beleza! Mas quem é ?
Passo 3
POW! Como já comentamos, é o módulo do vetor que é o momento linear da partícula :
Ou seja... .
Portanto, a gente conclui que...
POW! Mas é um vetor. Qual que é a direção e sentido dele?
Passo 4
Para responder essa pergunta aí, a gente pode observar que quando a partícula 3 bater na haste essa colisão vai causar um giro na haste no sentido anti-horário:
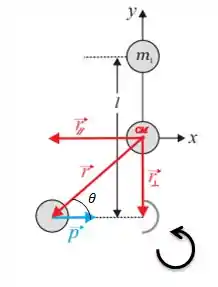
Pela regra da mão direita então, o momento angular que vai causar esse giro será...
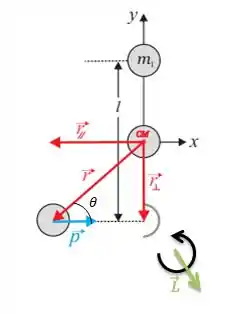
Ou seja... Saindo da sua telinha na direção do eixo :
Portanto, como comentamos no passo 1 será...
Precisamos agora achar o momento de inércia . Bora?
Passo 5
Considerando agora que a partícula 3 já está na haste e girando com a velocidade angular ao redor do centro de massa.
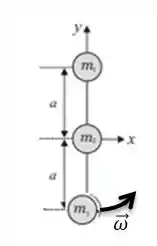
Quem é o momento de inércia nessa condição? Pow, de acordo com a teoria, o momento de inércia de um sistema de partículas é...
Onde é a distância de cada massa ao eixo de rotação, no caso, ao centro de massa que passa em cima da partícula . Assim...
Certo:
Passo 6
Belezinha! Então, podemos concluir que...
Como as massas forma dadas e valem cada...
Resposta
Letra C.