Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 412356789101112131415161718192021222324252627

Enunciado

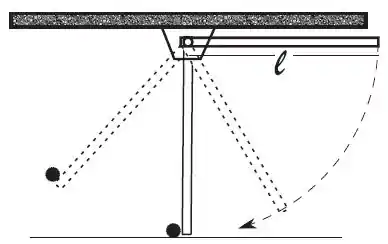
Uma haste homogênea e uniforme, de espessura desprezível, com massa M e comprimento l , pode girar sem atrito em torno de um pino que passa por uma de suas extremidades, como mostra a figura. O movimento da haste fica restrito a um plano vertical e o módulo da aceleração local da gravidade é igual a g .

  1. Sabendo-se que o momento de inércia da haste em relação a um eixo perpendicular à mesma, e que passe pelo seu centro de massa é igual a I C M = 1 / 12 M l 2 , calcule o momento de inércia da haste em relação ao eixo de rotação que passa pelo pino.
  2. Se a haste for liberada na posição horizontal, a partir do repouso, determine sua velocidade angular no instante que passa pela posição vertical.

    3. Ainda em relação à situação descrita no ítem anterior, considere que ao passar pela vertical, a exterminadade livre da haste se choque com um pequeno corpo de massa m = M / 9 , originalmente em repouso. O corpo de massa m adere à haste, e o conjunto continua em movimento de rotação em torno do pino.

  3. Calcule o momento de inércia do sistema haste-corpo após a colisão em relação ao pino.
  4. Qual é a velocidade angular do sistema haste-corpo de massa m , imediatamente após a colisão?

Passo 1

a)

Para achar o momento de inércia em relação ao eixo que ele pediu basta fazer o teorema dos eixos paralelos

I e i x o = I C M + M d 2

Nesse caso a distancia entre os eixos vai ser

d = l 2

Então

I e i x o = 1 12 M l 2 + M l 2 2

I e i x o = 1 12 M l 2 + 1 4 M l 2

I e i x o = 4 12 M l 2

I e i x o = M l 2 3

Passo 2

b)

Estamos em uma situação onde a energia mecânica da barra vai ser conservada, isso porque o atrito está sendo desconsiderado.

Inicialmente vamos ter

E m 0 = U 0

Lembra que quando fazemos a energia potencial pegamos a altura do centro de massa ?

Então

U 0 = M g h C M

U 0 = M g ⋅ l

Passo 3

A energia mecânica final vai ser

E m f = K f + U f

Onde

U f = M g h C M = M g ⋅ l 2 = M g l 2

E

K f = I C R ω f 2 2

Usamos aqui o momento de inécia em relação ao eixo de rotação

K f = M l 2 3 ⋅ ω f 2 2

Assim

E m f = M g l 2 + M l 2 ω f 2 6

Passo 4

Igualando as energias vamos ter

M g l 2 + M l 2 ω f 2 6 = M g l

M l 2 ω f 2 6 = M g l 2

ω f 2 = 3 g l

ω f = 3 g l

Passo 5

c)

O momento de inércia do sistema vai ser

I s i s t e m a = I b a r r a + I c o r p o

Já sabemos o momento de inércia da barra, e o corpo é uma partícula

I c o r p o = m d 2

Com

d = l

I c o r p o = M 9 ⋅ l 2 = M l 2 9

O momento de inércia do sistema fica

I s i s t e m a = M l 2 3 + M l 2 9

I s i s t e m a = 4 M l 2 9

Passo 6

d)

Repare que temos uma colisão onde o torque externo é zero. Então o momento angular se conserva. Vamos nos preocupar com o momento angular porque temos corpos girando. Vamos ter, antes da colisão

L s i s t e m a 0 = I b a r r a ⋅ ω f

L s i s t e m a 0 = M l 2 3 ⋅ 3 g l

Passo 7

Vamos chamar de ω ' a velocidade angular após a colisão. Então, depois da colisão

L s i s t e m a f = I s i s t e m a ⋅ ω '

L s i s t e m a f = 4 M l 2 9 ω '

Passo 8

Igualando os momentos angulares

4 M l 2 9 ω ' = M l 2 3 ⋅ 3 g l

ω ' = 3 4 3 g l

Resposta

  1. I e i x o = M l 2 3
  2. ω f = 3 g l
  3. I s i s t e m a = 4 M l 2 9
  4. ω ' = 3 4 3 g l

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .