Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 161234567891011121314151718192021222324252627

Enunciado

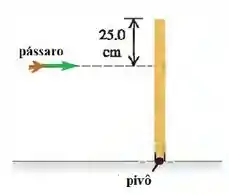
Um pássaro de massa m   =   500   g está voando horizontalmente a 2,25   m / s quando ele subitamente choca-se com uma barra vertical estacionária, atingindo-a 0,250   m abaixo de sua extremidade superior, conforme a figura. A barra é uniforme, tem L   =   0,750   m de comprimento, uma massa M   =   1,50   k g e pode girar sem atrito em torno do pivô. Imediatamente após a colisão, o pássaro cai verticalmente. Qual é a velocidade angular da barra imediatamente após ser atingida pelo pássaro? Use: Momento de inércia da barra em relação a um eixo que passa pelo pivô: I p i v ô = ( 1 / 3 ) M L 2

(A)   3,00   r a d / s  

(B)   2,00   r a d / s  

(C)   2,50   r a d / s  

(D)   3,50   r a d / s  

(E) 4,00   r a d / s

Passo 1

Temos que o pássaro irá transferir momento angular para a barra fazendo-a girar.

Pela conservação de momento angular temos que

L → a n t e s = L → d e p o i s

O momento angular antes da colisão é o momento angular do passáro

L → a n t e s = p → p a s s a r o × r → = p p a s s a r o × r b r a ç o   d e f o r ç a

O tamanho do braço de força do pássaro é distância vertical entre o centro de rotação e o pássaro

r b r a ç o   d e f o r ç a = 0,75 - 0,25 = 0,5   m

E o momento do pássaro é dado por

p p a s s a r o = m v = 0,5 × 2,25

p p a s s a r o = 1,1 25   K g . m / s

Assim o seu momento angular será dado por

L a n t e s = p p a s s a r o r b r a ç o d e   f o r ç a = 1,125 × 0 , 5

L a n t e s = 0,5625   K g . m 2 / s

Passo 2

O momento angular da barra logo após à colisão é dado por

L → d e p o i s = I ω → = M L 2 3 ω → = 1,5 × 0,75 2 3 ω →

L d e p o i s = 0,28125   ω

Passo 3

Assim

L → a n t e s = L → d e p o i s

0,5625 = 0,28125 ω

ω = 2   r a d / s

Resposta

(B)

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .