Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 612345789101112131415161718192021222324252627

Enunciado

Halliday & Resnick, Fundamentos de física, vol. 1: Mecânica. 9ª Ed. LTC, Rio de Janeiro. Cap 11, Questão 53

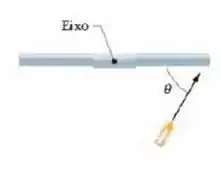
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma bala de 3 g é disparada, no plano de rotação, em direção a uma das extremidades. Vista de cima, a trajetória da bala faz um ângulo θ = 60 ° com a barra (figura abaixo). Se a bala se aloja na barra e a velocidade da barra é 10 r a d / s imediatamente após a colisão, qual é a velocidade da bala imediatamente antes do impacto?

Passo 1

O eixo de rotação está bem no centro da barra, então o raio de rotação é 0,25 m . Como antes do impacto não temos rotação da barra, apenas o movimento da bala é contabilizado.

Assim o momento angular inicial vai ser:

L i = m r v sen ⁡ 60 °

L i = 3 × 10 - 3 0,25 v   sen ⁡ 60 °

L i = v   6,49 × 10 - 4  

Passo 2

Na situação após o impacto, o momento de inércia do sistema vai ser a soma do momento da barra mais a da massa. Lembrando que o momento de inércia de uma barra é M R 2 / 12 teremos:

I f = M R 2 12 + m r 2

I f = 4 0,5 2 12 + 3 × 10 - 3 . 0,25 2

O momento angular final vai ser:

L f = I f ω f

E a velocidade angular final é 10   rad/s .

Passo 3

Agora podemos aplicar a conservação do momento angular:

L i = L f

6,49 × 10 - 4 v = 0,0835 × 10

v = 0,0835 × 10 6,49 × 10 - 4

v = 1,3 × 10 3   m/s

Resposta

v = 1,3 × 10 3   m/s

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .