Uma barra delgada homogênea e uniforme, de massa e comprimento , é articulada num pino , que passa por uma de suas extremidades, e pode girar sem atrito num plano vertical. Liberada a partir do repouso na posição horizontal, a barra sofre uma colisão elástica com um pêndulo ao passar pela posição vertical, como representa a massa de dimensões desprezíveis presa à extremidade da haste. O pêndulo também pode oscilar em torno do pino, sem atrito, no mesmo plano vertical que a barra. Sabe-se que o pêndulo encontrava-se em repouso antes da colisão com a barra, e que o momento de inércia da barra em relação ao eixo perpenducular ao plano vertical e que passa pelo pino é
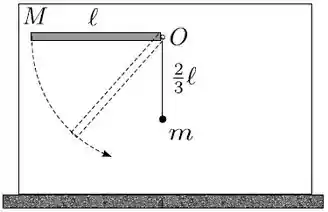
- Determine a velocidade angular da barra, , imediatamente antes da colisão com o pêndulo.
- Quais das seguintes grandezas: o momento linear e o momento angular em relação a são conservadas na colisão? Justifique a sua resposta.
- Determine a velocidade angular da barra, , imediatamente após a colisão.
- Determine o valor da razão para que a barra permaneça em repouso depois da colisão.
Passo 1
a)
Para acharmos a velocidade angular antes da colisão, vamos usar a conservação de energia mecânica. Isso é possível porque não temos forças dissipativas, tipo o atrito, atuando.
Inicialmente vamos ter
Lembra que quando fazemos a energia potencial pegamos a altura do centro de massa ?
Então
Passo 2
A energia mecânica final vai ser
Onde
E
Usamos aqui o momento de inécia em relação ao eixo de rotação
Assim
Passo 3
Igualando as energias vamos ter
Passo 4
b)
Não teremos forças externas nem torques externos atuando, isso nos diz que tanto o momento linear quanto o momento angular em relaçã a será conservado.
Passo 5
c)
Vamos nos preocupar com o momento angular porque temos corpos girando. Vamos ter, antes da colisão
Passo 6
Vamos chamar de a velocidade angular da barra após a colisão e a velocidade angular do pendulo após a colisão. Então, depois da colisão
Precisamos então achar o momento de inércia do corpo e o corpo é uma partícula, então
Com
O momento angular do sistema após a colisão fica
Passo 7
Igualando os momento angulares antes e depois da colisão, vamos deixar a velocidade angular inicial como só para facilitar as contas
Só essa equação não resolve o nosso problema.
Passo 8
O enunciado disse que a colisão é elástica, isso nos diz que a energia cinética vai ser conservada durante a colisão.
A energia cinética antes da colisão vai ser
A energia cinética depois da colisão fica
Igualando as energias
Passo 9
Temoso sistema
Que lindo esse menino né? SQN. Esse sistema é bem complicado de resolver, então vamos a “matemágica”
Vamos começar dividindo as duas equações por
Vamos ter, pela primeira equação
Na segunda equação
Substituindo a subtração vamos ter
Encontrando
Passo 10
Vamos substituir o valor de encontrado no fim do passo na primeira equação
Agora substituímos o valor de
Passo 11
d)
A barra permanecer em repouso significa que a velocidade angular depois da colisão é zero
É o mesmo que
Resposta
- Não teremos forças externas nem torques externos atuando, isso nos diz que tanto o momento linear quanto o momento angular em relaçã a será conservado.