Origem do Exercício
Uma barra de comprimento próprio move-se com velocidade constante relativamente ao sistema conforme a figura.
A extremidade da barra passa pela origem de no instante . Nesse instante é emitido de um sinal de luz que viaja de para .
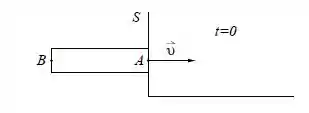
- Em que instante medido num referencial em repouso em relação à barra o sinal chega a ?
- Em que instante medido no referencial o sinal chega a ?
Passo 1
Letra a)
Para um referencial em repouso em relação à barra o sinal atingirá no instante:
Pois o comprimento próprio é o comprimento medido no referencial da barra.
Passo 2
Letra b)
Para acharmos o instante medido no referencial usamos a contração do comprimento da barra:
Onde:
A distância percorrida pela nave até a luz atingir o ponto foi
Assim, o tempo que a luz leva para chegar ao fundo da nave é de:
Rearrumando:
Mas podemos tentar tirar esse da equação abrindo ele:
E com isso, teremos:
Ou seja
Resposta
Letra a)
Letra b)
Exercícios de Livros Relacionados
50. Um cubo de metal cuja aresta possui comprimento a está em repouso em um sistema de referência S com uma de suas arestas paralelas ao eixo O x . Logo, em S o volume do cubo é a 3 . O sistema de ref
Um astrônomo na Terra observa um meteoroide no céu do hemisfério sul se aproximando da Terra a uma velocidade de 0,800 c . No momento de sua descoberta o meteorito está a 20,0 anos-luz da Terra. Calcu
Um amigo passa por você em uma nave espacial que se move em alta velocidade. Ele lhe diz que sua nave possui 20,0m de comprimento e que a nave idêntica na qual você está sentado mede 19,0m . Segundo s
Com que velocidade uma trena precisa se mover se seu comprimento for medido com um encolhimento de 0,500m ?
Uma nave espacial com comprimento próprio de 300m passa por um observador na Terra. Segundo esse observador, leva 0,750μ s para a nave espacial passar por um ponto fixo. Determine a velocidade da nave