Física 4 – UFRJ – 2019.2 – P2 – Questão 4
Um triângulo retângulo está em repouso em relação a um referencial inercial e possui área . Os lados do triângulo que são ortogonais entre si possuem o mesmo comprimento , no qual um lado é paralelo ao eixo e o outro paralelo ao eixo , em relação a . O referencial se move com velocidade em relação a . Determine a área desse triângulo em relação ao referencial inercial .
a) .
b) .
c) .
d) .
Passo 1
Fala pessoal, bora resolver essa questão sobre contração do espaço?
O triângulo está parado com relação a ao referencial e um referencial se move com velocidade a direção com relação . A seguir faço um esboço dessa situação:
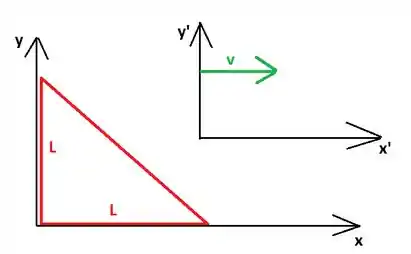
No referencial , a área do triângulo é
Queremos saber a área no referencial . Para isso, temos que achar os lados do triângulo medido no referencial . Como o referencial se move na direção , as dimensões na direção não são alteradas, de modo que o lado vertical do triângulo segue sendo :
Mas e o lado horizontal?
Passo 2
Para achar o lado horizontal usamos a contração do espaço:
Nessa equação, (comprimento próprio) é o lado medido no referencial em que o corpo está em repouso. Portanto, é o lado no referencial , isto é, . Já o fator é calculado por
Assim,
No referencial o lado horizontal é metade do que ele é no referencial A. Assim, a área será
Portanto, temos que assinalar a alternativa A.
Resposta
Alternativa A.