Marque X na escolha correta e a justifique. Dois eventos ocorrem a 100 m de distância, separados por um intervalo de tempo de 0,60 μs. Obtenha a velocidade de um referencial no qual esses eventos ocorrem no mesmo ponto do espaço. Note que c representa a velocidade da luz.
1-( ) 0,18 c.
2-( ) 0,25 c.
3-( ) 0,56 c.
4-( ) 0,82 c.
Passo 1
Nessa questão temos que tomar o seguinte cuidado, ele quer que determinemos a velocidade desse referencial para que esses pontos que estão a 100m de distancia um do outro ocorram no mesmo ponto do espaço, ou seja, se trata de uma questão de contração do comprimento, como assim?
Queremos saber a velocidade que o referencial deve estar até que o comprimento do primeiro referencial se reduza a zero, ou seja, vamos relembrar a fórmula tomando o seguinte cuidado.
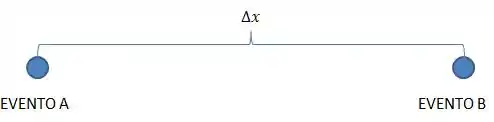
Quando os referenciais estão em repouso sabemos que podemos representa-los dessa forma, mas e se atribuirmos a um referencial uma velocidade o que ocorrerá?
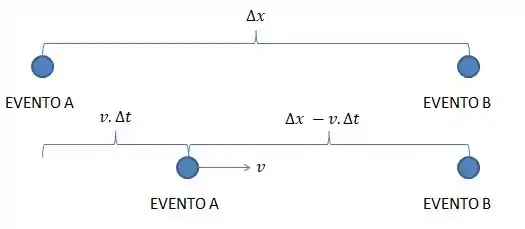
Observamos na figura que quando o referencial estiver a uma velocidade terá percorrido uma distancia de . lembrando que
sabendo disso, o que o problema quer que façamos é que peguemos a distancia entre os referencias no segundo caso e façamos que ela se contraia até zero.
Vamos entender isso então.
Passo 2
Nossa fórmula de contração é dada por
Em que é o fator de Lorentz e é quanto que um referencial precisa percorrer em relação ao outro.
Dessa forma teremos
Mas lembra que nosso tem que ser levado até zero? Fazendo isso teremos
Em que
Passo 3
Mas queremos isso em função da velocidade da luz, então basta dividir a resposta por .
Com isso teremos
Resposta
3-( x )