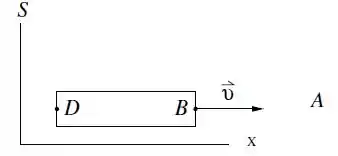
Uma espaçonave de comprimento próprio move-se com velocidade com e passa por um observador em repouso no ponto A do eixo x do sistema de coordenadas S, conforme indicado na figura. O observador registra em seu relógio um intervalo de tempo para a passagem da espaçonave por ele, isto é, o intervalo de tempo entre a passagem de B e D pelo ponto A. Calcule a velocidade expressando sua resposta somente em termos de e dos parâmetros e
Passo 1
Vamos considerar o referencial S em repouso com o observador do ponto A e outro referencial S’ que se move com a mesma velocidade da espaçonave.
Para o observador em repouso em S, o intervalo de tempo da passagem da espaçonave entre os pontos B e D vale:
sendo:
devido à contração dos comprimentos e o comprimento próprio ser medido pelo observador na espaçonave.
Passo 2
Então, substituindo:
Como precisamos isolar o v, vamos elevar os dois lados ao quadrado: