Uma barra de comprimento próprio L, orientada segundo um ângulo em relação ao eixo
x está em repouso em um sistema inercial S, conforme a figura. Considere um sistema S’
que se move com velocidade constante em relação a S. Nos itens abaixo expresse
suas respostas em termos de L, , , e da velocidade da luz c.
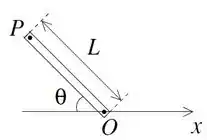
(a) Qual é o comprimento L’ da barra no sistema S’?
(b) Qual é o ângulo de orientação da barra no sistema S’?
Passo 1
No primeiro item da questão é pedido o comprimento L’ da barra. Para isso precisamos analisar o funcionamento da nossa barra no referencial S’, pelo desenho conseguimos compreender como que um referencial se move em relação ao outro.
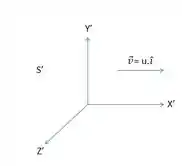
Vamos primeiro decompor a nossa barra L e analisar cada uma das suas componentes no referencial S’
Passo 2
Primeiro faremos a decomposição no referencial S
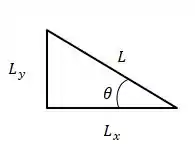
Passo 3
Feito a decomposição no referencial S vamos analisa-los no referencial S’
Sabemos que
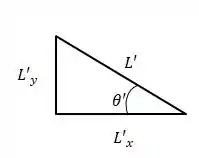
Mas perceba o seguinte, no Referencial S’ não temos velocidade na direção y, logo, concluímos que nada ocorre de diferente nessa direção, então podemos afirmar que
Porém no referencial S’ temos velocidade na direção x, logo, lembrando da teoria, sabemos que ocorre uma contração da distância, dada pela fórmula
Dessa forma a nossa componente em x será
Passo 4
Sabendo quanto vale e calculamos facilmente o valor de L’
Fazendo as devidas relações e mudanças, no fim chegamos a conclusão que L’ vale
Passo 5
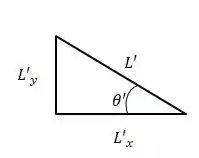
Agora na questão b queremos descobrir quanto vale a nosso ângulo que a barra faz com o nosso eixo x’, olhando a barra no referencial S’ teremos
Dessa forma usando a relação trigonométrica teremos
Resposta
a)
b)