Uma espaçonave de comprimento próprio move-se com velocidade em relação ao sistema inercial . De acordo com um observador em repouso em a espaçonave leva um intervalo de tempo igual a para passar pela origem de , conforme a figura.
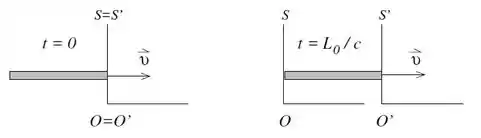
- Calcule o módulo da velocidade da espaçonave em termos de
- Calcule o intervalo de tempo para a passagem da espaçonave pela origem no referencial da espaçonave.
Passo 1
Letra a)
Para calcularmos a velocidade da espaçonave de acordo com o referencial , temos que usar o comprimento e o tempo , ambos medidos por ele próprio. Assim, teremos:
Onde , sendo o comprimento próprio da barra, é medido pelo referencial onde ela está em repouso .
Pelo fenômeno da contração do comprimento, temos:
Substituindo:
Sendo que o fator de Lorentz é definido como:
Teremos:
Passo 2
Letra b)
No referencial da barra , para medir o tempo que o ponto do observador em demora para passar por toda a barra, é necessário um relógio nas duas extremidades dela.
Já no referencial , basta um relógio na origem (os dois eventos ocorrem no mesmo ponto).
Isso significa que é o referencial que mede o tempo próprio. Assim, pela dilatação do tempo, temos:
No passo anterior, encontramos que:
Vamos encontrar a alma gêmea do :
Assim, temos então que:
Resposta
Letra
Letra