. Um anel circular de plástico, de raio , situa-se no plano com seu centro coincidente com a origem. O anel possui uma carga uniformemente distribuída ao longo da semicircunferência pertencente ao primeiro e segundo quadrantes e uma carga uniformemente distribuída o longo da semicircunferência pertencente ao terceiro e quarto quadrantes. Escolhendo o potencial elétrico como zero no infinito, quais valores melhor aproximam o potencial e o módulo do campo elétrico produzidos pelo anel em seu centro, respectivamente?
Dados: e .
Escolha uma opção:
e
e
e
e
e
e
e
e
Passo 1
Vem comigo que gente detona com essa questão juntos!
O anel tem metade dele com um certo valor de carga e a outra metade com outro valor de carga, então cada metade vai produzir um campo elétrico diferente.
Então temos que a achar uma expressão para o campo no centro de uma metade de arco, tendo essa expressão a gente aplica para cada lado do nosso arco.
Para isso vamos usar o seguinte:
A nossa situação é da seguinte forma:
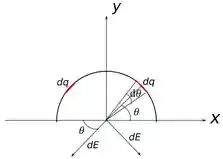
Olhando a figura do que temos o mesmo elemento de carga que temos de uma lado da metade do arco temos do outro lado, então a componente dos campos que eles produzem na direção se cancelam, logo só temos campo na direção , logo temos que:
Então temos que achar usando aquela equação que mostrei acima.
Para calcular o potencial elétrico vamos usar o seguinte:
Onde nós já definimos mais acima e é a distância do anel até o ponto que queremos saber o potencial.
Passo 2
Antes de partirmos para o cálculo da integral de , temos que encontrar uma expressão para primeiro. Vamos usar a definição de densidade linear de cargas, que é carga por unidade de comprimento, então:
Onde é um elemento de comprimento da metade do anel, podemos relacionar esse com usando o seguinte:
Onde é o raio do anel, então temos que:
Então nossa expressão para fica da seguinte forma:
Passo 3
Agora vamos calcular , temos:
Então temos que:
Antes a gente viu que lambda é a densidade linear de carga, então ele pode ser igual a carga total dividida pelo comprimento da metade do anel, assim:
Então:
Usando que , temos que:
Pronto, chegamos em uma expressão para o módulo do campo produzido pela metade de um anel, então vamos aplicar isso para as duas metades que temos, o que vai mudar de uma para outra é a carga de cada metade.
Passo 4
Para e usando os outros valores que temos, ficamos com:
Agora para a metade com carga , temos:
Somando em módulo os dois campos, temos que o campo no centro do anel vai ser dado por:
Passo 5
Agora vamos achar o potencial, temos o seguinte:
Usando o que conhecemos, temos:
Usando o que sabemos para , temos:
Lembrando que varia de a , temos:
Então temos que:
Onde nesse caso vai ser a carga total do anel, logo , assim temos:
Então nossa alternativa correta é a letra .
Resposta
e