Uma esfera centrada na origem tem raio e a seguinte distribuição de cargas em seu volume:
Onde é uma constante negativa. Calcule a carga contida no interior de uma superfície esférica imaginária centrada na origem com raio , se:
Passo 1
Desenhando o primeiro caso chegamos à seguinte figura:
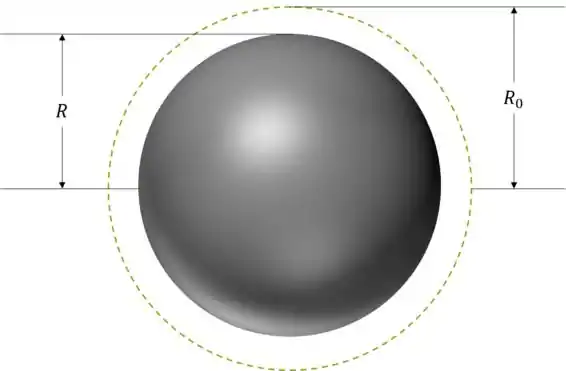
No caso a superfície esférica imaginária está representada somente em corte e com uma linha pontilhada. Não sou sinistro no PowerPoint que nem o Brunão da Física IV.
Passo 2
Do desenho podemos observar que toda a carga que está contida dentro da superfície imaginária é a carga total da esfera, portanto resolvemos o item assim:
Trocando o diferencial de carga utilizando a definição da densidade:
E trocando o diferencial de volume por seu correspondente em coordenadas polares:
Podemos substituir na fórmula e fazer a conta.
Passo 3
Substituindo:
Arrumando:
E finalmente calculamos:
Item respondido!
Passo 4
Agora precisamos desenhar a situação do item :
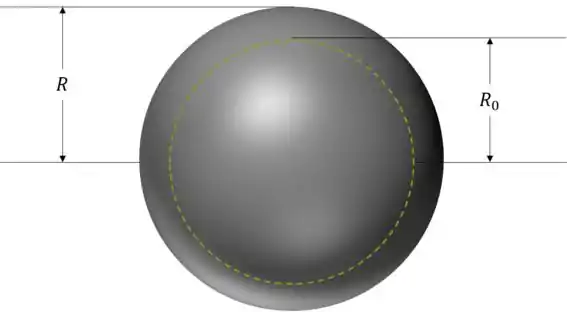
Perfeito. Podemos ver que a carga encerrada no interior da superfície esférica imaginária não é igual à carga total da esfera, e sim um valor menor em módulo.
Como resolver? Somamos apenas os elementos infinitesimais de carga no interior da superfície imaginária:
Pela mesma lógica de antes, substituímos os dados:
E obtemos o resultado:
E acabou.