Uma casca esférica condutora de raio interno e externo é carregada com uma carga . Além disso, uma carga pontual é colocada no centro da casca esférica.
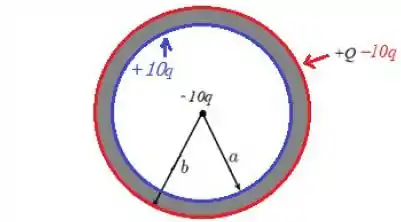
Qual é a densidade de carga na superfície externa da casca esférica?
Passo 1
O primeiro trabalho que temos aqui é determinar as cargas nas superfícies interna e externa da casca esférica.
Quando temos uma carga no interior da casca esférica (nesse caso, a carga pontual ), a carga na superfície interna tem o módulo igual ao da carga no interior da casca, mas sinal oposto, logo:
Para determinar a carga na superfície externa precisamos lembrar que a soma desta com a carga na superfície interna deve ser igual à carga total da casca , logo:
Passo 2
Por fim, a densidade de carga na superfície externa é dada por:
Onde corresponde à área da superfície externa, que é a área da esfera de raio , ou seja,
Assim
Resposta