A Figura abaixo mostra uma semicircunferência de raio com uma carga positiva distribuída conforme a seguinte densidade linear , com sendo uma constante. Nessas circunstâncias, qual é a carga total da semicircunferência?
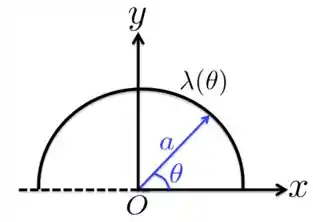
Passo 1
Para encontrarmos o valor da carga total , precisamos resolver a seguinte integral:
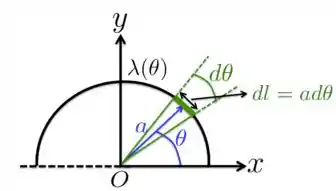
Como mostramos na Figura acima, o elemento de comprimento é dado por . Se substituímos isso na integral juntamente com , ficamos com
Disso, vamos chegar à seguinte expressão para a carga total
Resposta
Exercícios de Livros Relacionados
Uma fina casca esférica não condutora, uniformemente carregada, com raio R , tem uma carga total positiva igual a Q ; Um pequeno pedaço é removido da superfície. (a) Quais são o módulo, a direção e o
Duas placas metálicas quadradas idênticas têm, cada uma, área de 500c m 2 . Elas são separadas por 1,50c m e estão, ambas, inicialmente descarregadas. A seguir, uma carga de + 1,50n C é transferida da
Uma lâmina plana infinita não condutora tem uma densidade superficial de carga + 3,00μ C / m 2 e está no plano y = - 0,600m . Uma segunda lâmina plana infinita tem densidade superficial de carga de -
O pequeno segmento de fio na FIGURA Q27.4 contém 10n C de carga. a. O segmento é reduzido a um terço do comprimento original. Qual é a razão λ f / λ i , onde λ i e λ f são as densidades de carga inici
Um disco circular está carregado e sua uma densidade superficial de carga vale 8n C / c m ² ² . Qual será a densidade superficial de carga se o raio do disco for dobrado?