UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 11a
11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.
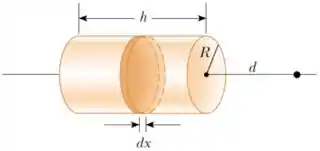
(a) Determine a densidade superficial de carga do cilindro.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nessa questão temos uma casca cilíndrica com raio , comprimento e carga que é distribuída uniformemente.
Com isso, queremos descobrir qual é a densidade superficial de carga do cilindro.
Tem ideia de como fazer isso? 👀
A densidade superficial de cargas é dada por
Assim, podemos calcular a densidade superficial de carga.
Bora lá! 😬
Passo 2
Foi dito que a casca cilíndrica é isolante e tem uma distribuição de cargas uniforme.
Dessa forma, para obter a densidade de cargas é dada pela área total da casca.
A área da casca cilíndrica é dada por
Portanto, substituindo na fórmula da densidade
Sacou como faz? Responde Aí! 😉
