Observe a figura abaixo:
Dado que esse anel tem raio , digamos que a densidade de carga linear dele seja:
Onde é o ângulo trigonométrico, medido à partir do eixo no sentido anti-horário e é uma constante arbitrária. A questão é: qual a carga total do anel?
Passo 1
A densidade de carga linear não significa que vamos estar sempre integrando em uma barra reta. Linear significa somente que estamos integrando em uma dimensão só.
Bom, o início do esquema é sempre o mesmo:
Agora integramos em todo o anel:
Show. A função nós temos, agora falta identificar esse e o nosso domínio de integração, que ainda está meio misterioso.
Passo 2
Estamos usando um sistema de coordenadas cartesianas, quem deve ser o nosso ? Seria ou ? Ou nenhum dos dois? Só conseguimos responder isso se entendermos o que de fato é o diferencial de comprimento : ele é um pedaço infinitesimal do anel.
Ou seja, não pode ser nem nem . O único jeito de tratar esse comprimento infinitesimal é com coordenadas polares:
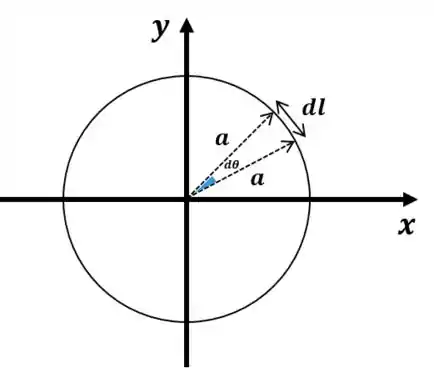
Agora sim, podemos então escrever:
Passo 3
E em função de nós sabemos escrever nosso domínio de integração. Portanto:
Logo:
A carga total deu zero, sendo que ela não é nula em todos os pontos. Pode isso, produção? Claro que pode, ora. Basta que a quantidade de cargas positivas seja igual à quantidade de cargas negativas. Que é exatamente o que acontece. Como podemos observar pela característica da função seno:
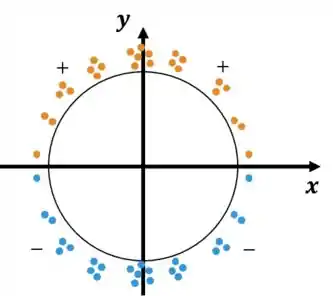
Podemos perceber que a carga total vai dar zero.
Isso encerra como calcular a carga de barras curvas circulares, é só trocar para coordenadas polares.