Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 1712345678910111213141516181920212223242526272829

Enunciado

Corpos Rígidos

Uma placa homogênea que era quadrada tem sua área reduzida de um quarto, conforme a figura.

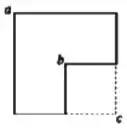
Os momentos de inércia em relação a eixos perpendiculares ao plano da placa e que passam pelos pontos a , b e c são, respectivamente, I a , I b e I c . Pode-se afirmar que:

  1. I a = I b = I c
  2. I a > I b > I c
  3. I c > I a > I b
  4. I a = I b > I c
  5. I a = I b < I c

Passo 1

Bem, vamos começar dividindo essa nova placa em formato de L em 3 placas iguais de lado L ? Assim fica bem mais fácil calcular o centro de massa do novo conjunto.

Vamos lá.

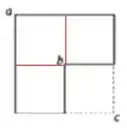
Os quadrados da esquerda tem o centro de massa do eixo x em x = L / 2   e o quadrado da direita tem o centro de massa do eixo x em x = 3 L / 2 .

Os quadrados de cima tem o centro de massa do eixo y em y = 3 L / 2   e o quadrado de baixo tem o centro de massa do eixo y em y = L / 2 .

Com isso, calculamos o centro de massa do conjunto.

Em x :

x C M = 2 ∙ M 4 ∙ L 2 + M 4 ∙ 3 L 2 3 M 4

x C M = 5 6 L

Em y :

y C M = 2 ∙ M 4 ∙ 3 L 2 + M 4 ∙ L 2 3 M 4

y C M = 7 6 L

Passo 2

Consegue visualizar no desenho mais ou menos onde se encontra o centro de massa da nova placa em formato de L?

Agora é só pensar nos teorema dos eixos paraleros que diz:

I = I C M + M d 2

Para todos os 3 eixos que precisamos estudar, teremos I C M e M constantes, basta, então, estudarmos a distância d do centro de massa até os pontos a , b e c .

Temos que

d b < d a < d c

Logo,

I c > I a > I b

Resposta

Letra c)

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.