Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 3124567891011121314151617181920212223242526272829

Enunciado

Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56   k g , em relação a um eixo perpendicular à uma régua na marca de 20   c m . (Trate a régua como uma barra fina.)

Passo 1

Neste problema nos foi pedido o momento de inércia em relação a um eixo que não passa pelo centro de massa do corpo, portanto, iremos usar o teorema dos eixos paralelos.

Dá uma olhada na imagem pra facilitar a aplicação:

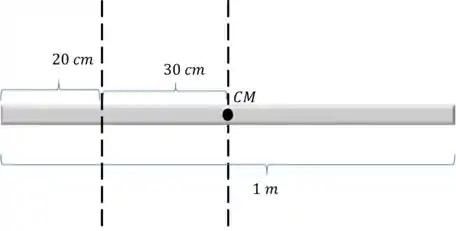
Passo 2

Nós sabemos que o valor do momento de inércia da régua é igual ao momento de inércia de uma barra homogênea, portanto, o seu I 0 , aquele momento de inércia calculado em relação ao eixo que passa pelo centro de massa é dado por:

I 0 = M L 2 12

Queremos o momento de inércia em relação à um eixo que, como na imagem, dista 30   c m do eixo que passa pelo centro de massa, portanto:

d = 0,3   m

E então, aplicando o teorema, temos:

I = I 0 + M d 2

I = 0,56   .   1 2 12 + 0,56   .   0,3 2

I ≅ 0,097   k g . m 2

Resposta

I ≅ 0,097   k g . m 2

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.