Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 2912345678910111213141516171819202122232425262728

Enunciado

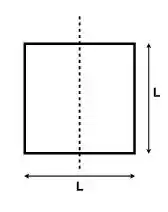
Um objeto é formado por quatro barras delgadas homogêneas, cada uma com massa M e comprimento L , na forma de um quadrado. O momento de inércia em relação ao eixo representado pela linha pontilhada na figura e passando pelo plano do objeto é:

(a) 1 3 M L 2

(b) 2 3 M L 2

(c) 4 3 M L 2

(d) nenhuma das alternativas

(e) 32   M L 2

Passo 1

Ele tá pedindo pra gente calcular o momento de inércia desse corpo em relação àquele eixo.

Como o objeto é formado por barras, logo não são partículas, elas possuem a massa distribuída em toda extensão, então temos aqueles valores tabelados já.

E o momento de inércia do objeto é a soma dos momentos de inércia de cada barra!

Passo 2

Então, vamos separar o nosso objeto em 4 barrinhas:

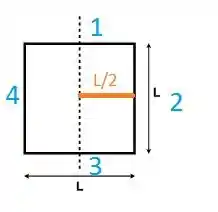
Então:

I T = I 1 + I 2 + I 3 + I 4

O momento de inércia de uma barra que gira ao redor de um eixo passando pelo centro de massa é uma valor tabelado e vale I = M L 2 12

Olhando pra nossa figura, o eixo passa pelo centro das barras 1 e 3. Então o momento de inércia delas é moleza:

I 1 = I 3 = M L 2 12

Show...Mas em relação ao momento de inércia das barras 2 e 4? Não tem eixo passando por elas! E agora???

Passo 3

Agora a gente usa o famoso teorema dos eixos paralelos:

I P = I C M + M d 2

Calma, é só seguir alguns passos que você vai ver que é moleza:

i) Identificar o eixo de rotação

Beleza, é aquele vertical pontilhado.

ii) Identificar qual é a distância do eixo de rotação para o eixo que passa pelo centro de massa, esse que é o d .

Fizemos isso ali na figura, a distância entre o eixo de rotação, que é o pontilhado, até um eixo passando pelo centro de massa da barra (em vermelho) é L / 2

iii) Calcular o momento de inércia para o eixo que passa pelo CM, o vermelho.

Como a barra tá em cima do eixo, então I C M = 0 .

iv) Aplicando o teorema:

I P = I C M + M d 2

I P = 0 + M L 2 2

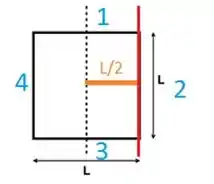
Como as barras 2 e 4 estão a mesma distância L / 2 do eixo central e o momento de inércia delas em relação a um eixo passante no CM é zero, então:

I 2 = I 4 = M L 2 2

I 2 = I 4 = M L 2 4

Passo 4

Agora já podemos descobrir o momento de inércia total:

I T = I 1 + I 2 + I 3 + I 4

I T = M L 2 12 + M L 2 4 + M L 2 12 + M L 2 4

Resolvendo isso daí:

I T = 2 M L 2 3

Resposta

Alternativa B

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.