Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 6123457891011121314151617181920212223242526272829

Enunciado

Momento de Inércia

Uma haste fina e uniforme com uma massa 6 m é dobrada para formar um hexágono regular de lado a . Qual é o momento de inércia do hexágono em torno do eixo que passa pelo seu centro e é perpendicular ao plano formado pelo hexágono? Considere que o momento de uma haste fina de comprimento L é dado por I = 1 12 M L 2 .

a ) 5   m a 2

b ) 5 m a 2 6

c ) 5 m a 2 3

d ) 6   m a 2

e ) 6 m a 2 5

Passo 1

Podemos escarar esse hexágono como 6 barras, cada uma de massa m e I c m = 1 12 m a 2 . Para encontrar o momento de inércia em relação ao centro C do hexágono, teremos que utilizar o teorema dos eixos paralelos:

I C = I c m + m d 2

Onde d é a distância do centro de massa da barra ao centro do hexágono, que nada mais é que a altura de um triângulo:

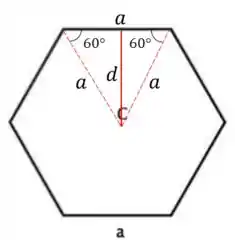
A distância d pode ser calculada como:

d = a sen ⁡ 60 °

d = a 3 2

Substituindo no momento de inércia:

I C = I c m + m d 2

I C = 1 12 m a 2 + m a 3 2 2

I C = 1 12 m a 2 + 3 4 m a 2

I C = 10 12 m a 2

Este é o momento de inércia de cada barra em relação ao centro C do hexágono. Basta agora calcular o momento total, que nada mais é que somar o momento de todas as 6 barras.

I t o t a l = 6 . 10 12 m a 2

I t o t a l = 5 m a 2

Resposta

Alternativa a

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.